 por Louis » Seg Jul 09, 2012 23:56
por Louis » Seg Jul 09, 2012 23:56
Olá, já quebrei a minha cabeça de todas as formas possíveis com esta questão. Com o objetivo de mostrar o gráfico da função tirei uma foto.
Agradeço a ajuda.
- Anexos
-

-
Louis
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Jul 09, 2012 17:48
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Ter Jul 10, 2012 00:28
por e8group » Ter Jul 10, 2012 00:28
Oque você tentou ?
Note que
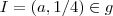
e

isto implica que
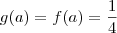
ou seja ,basta encontrar o valor para a qual a imagem da função g e f equivale a 1/4 .
Uma vez encontrado o valor para

tal que

,em consequência obterá k .Pois

. Daí para concluir o exercício basta calcular
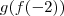
que é equivalente a

já que
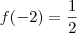
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Louis » Ter Jul 10, 2012 10:05
por Louis » Ter Jul 10, 2012 10:05
Estava tentando isolar o x para depois substituí-lo na função, pelo visto estava me guiando pelo caminho errado. Como faço para encontrar o valor para a qual a imagem da função g e f equivale a 1/4?
-
Louis
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Jul 09, 2012 17:48
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Russman » Ter Jul 10, 2012 10:20
por Russman » Ter Jul 10, 2012 10:20
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por e8group » Ter Jul 10, 2012 10:47
por e8group » Ter Jul 10, 2012 10:47
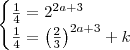
Por um lado temos :
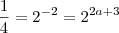
como temos as bases da igualdade iguais(caso não acredite aplique logaritmo de mesma base em ambos lados da igualdade )
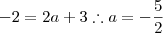
.Entretanto por outro lado:
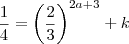
,lembrando que
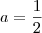
,temos :

,ou seja
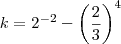
.Daí só calcular
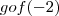
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Louis » Ter Jul 10, 2012 11:22
por Louis » Ter Jul 10, 2012 11:22
Santhiago, se de acordo com as funções que você comparou, o resultado do a obtido foi -5/2, por que quando você substituiu este valor para encontrar o k você considerou como sendo 1/2? Obrigado por esclarecer como você chegou até o resultado, se não dissesse que aplicou as bases da igualdade, ficaria perdido. Tentei calcular o gof (-2), mas não creio estar fazendo a conta do jeito certo, isso porque encontrei um intervalo correspondente ao do número 4 e acabo de conferir que a resposta certa é o número 2.
Obrigado Russman por ter postado.
-
Louis
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Jul 09, 2012 17:48
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Ter Jul 10, 2012 12:29
por e8group » Ter Jul 10, 2012 12:29
Louis escreveu:Santhiago, se de acordo com as funções que você comparou, o resultado do a obtido foi -5/2, por que quando você substituiu este valor para encontrar o k você considerou como sendo 1/2? Obrigado por esclarecer como você chegou até o resultado, se não dissesse que aplicou as bases da igualdade, ficaria perdido. Tentei calcular o gof (-2), mas não creio estar fazendo a conta do jeito certo, isso porque encontrei um intervalo correspondente ao do número 4 e acabo de conferir que a resposta certa é o número 2.
Oops !
Não sei porque fiz isso (haha) ....
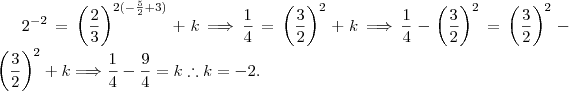
Assim , temos :
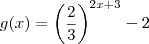
Ou seja :

como

a resposta é (02) .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Louis » Ter Jul 10, 2012 13:10
por Louis » Ter Jul 10, 2012 13:10
(risos). Uma última pergunta sobre a questão. Como você chegou a conclusão que f(-2) = 1\2?
-
Louis
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Jul 09, 2012 17:48
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Ter Jul 10, 2012 18:36
por e8group » Ter Jul 10, 2012 18:36
Louis escreveu:(risos). Uma última pergunta sobre a questão. Como você chegou a conclusão que f(-2) = 1\2?
pela lei de formação de

temos que :

então
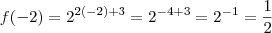
OK !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- duvida em funcoes
por bmachado » Qua Fev 29, 2012 00:33
- 2 Respostas
- 1559 Exibições
- Última mensagem por bmachado

Qua Fev 29, 2012 16:51
Funções
-
- [Funções] Pequena dúvida
por Renato_RJ » Sex Jan 13, 2012 19:44
- 4 Respostas
- 2566 Exibições
- Última mensagem por Renato_RJ

Sáb Jan 14, 2012 18:06
Funções
-
- [funcoes e geometria] duvida
por telmojc » Qua Mar 21, 2012 14:06
- 0 Respostas
- 849 Exibições
- Última mensagem por telmojc

Qua Mar 21, 2012 14:06
Funções
-
- Dúvida Geometria e Funções
por Andrewo » Seg Mar 26, 2012 09:10
- 0 Respostas
- 717 Exibições
- Última mensagem por Andrewo

Seg Mar 26, 2012 09:10
Funções
-
- [Funções] Dúvida Urgente
por epbittencourt » Sex Jun 01, 2012 15:55
- 1 Respostas
- 1799 Exibições
- Última mensagem por Molina

Sex Jun 01, 2012 16:55
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



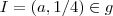 e
e  isto implica que
isto implica que 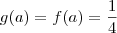 ou seja ,basta encontrar o valor para a qual a imagem da função g e f equivale a 1/4 .
ou seja ,basta encontrar o valor para a qual a imagem da função g e f equivale a 1/4 .  tal que
tal que  ,em consequência obterá k .Pois
,em consequência obterá k .Pois  . Daí para concluir o exercício basta calcular
. Daí para concluir o exercício basta calcular 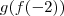 que é equivalente a
que é equivalente a  já que
já que 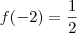



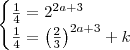
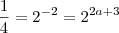 como temos as bases da igualdade iguais(caso não acredite aplique logaritmo de mesma base em ambos lados da igualdade )
como temos as bases da igualdade iguais(caso não acredite aplique logaritmo de mesma base em ambos lados da igualdade )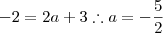 .Entretanto por outro lado:
.Entretanto por outro lado: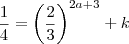 ,lembrando que
,lembrando que 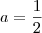 ,temos :
,temos : ,ou seja
,ou seja 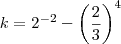 .Daí só calcular
.Daí só calcular 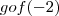


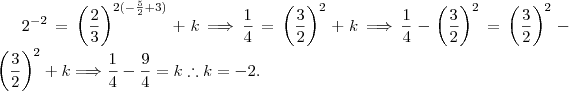
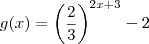

 a resposta é (02) .
a resposta é (02) .

 temos que :
temos que :  então
então 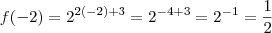 OK !
OK !
