Olá, já quebrei a minha cabeça de todas as formas possíveis com esta questão. Com o objetivo de mostrar o gráfico da função tirei uma foto.
Agradeço a ajuda.



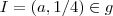 e
e  isto implica que
isto implica que 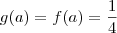 ou seja ,basta encontrar o valor para a qual a imagem da função g e f equivale a 1/4 .
ou seja ,basta encontrar o valor para a qual a imagem da função g e f equivale a 1/4 .  tal que
tal que  ,em consequência obterá k .Pois
,em consequência obterá k .Pois  . Daí para concluir o exercício basta calcular
. Daí para concluir o exercício basta calcular 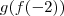 que é equivalente a
que é equivalente a  já que
já que 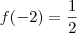



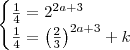
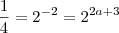 como temos as bases da igualdade iguais(caso não acredite aplique logaritmo de mesma base em ambos lados da igualdade )
como temos as bases da igualdade iguais(caso não acredite aplique logaritmo de mesma base em ambos lados da igualdade )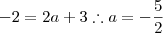 .Entretanto por outro lado:
.Entretanto por outro lado: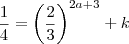 ,lembrando que
,lembrando que 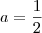 ,temos :
,temos : ,ou seja
,ou seja 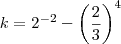 .Daí só calcular
.Daí só calcular 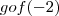


Louis escreveu:Santhiago, se de acordo com as funções que você comparou, o resultado do a obtido foi -5/2, por que quando você substituiu este valor para encontrar o k você considerou como sendo 1/2? Obrigado por esclarecer como você chegou até o resultado, se não dissesse que aplicou as bases da igualdade, ficaria perdido. Tentei calcular o gof (-2), mas não creio estar fazendo a conta do jeito certo, isso porque encontrei um intervalo correspondente ao do número 4 e acabo de conferir que a resposta certa é o número 2.
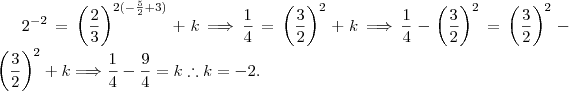
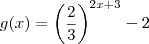

 a resposta é (02) .
a resposta é (02) .

Louis escreveu:(risos). Uma última pergunta sobre a questão. Como você chegou a conclusão que f(-2) = 1\2?
 temos que :
temos que :  então
então 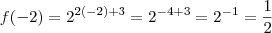 OK !
OK !
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)