
Eu tentei fazer invertendo a fração, tentei também com x em evidência, mas deu indeterminação.



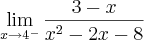
 ou
ou 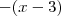


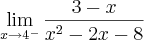



 ) por um número que se aproxima de
) por um número que se aproxima de  , ou seja, aproximando pela direita teríamos como resposta o mais infinito. Analogamente notamos que a divisão de uma constante por um número que se aproxima de
, ou seja, aproximando pela direita teríamos como resposta o mais infinito. Analogamente notamos que a divisão de uma constante por um número que se aproxima de 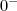 , ou seja, aproximando pela esquerda teríamos como resposta o menos infinito.
, ou seja, aproximando pela esquerda teríamos como resposta o menos infinito.
Claudin escreveu:Basta analisar que: dividir um número (uma constante no caso o) por um número que se aproxima de
, ou seja, aproximando pela direita teríamos como resposta o mais infinito. Analogamente notamos que a divisão de uma constante por um número que se aproxima de
, ou seja, aproximando pela esquerda teríamos como resposta o menos infinito.


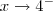 tende a
tende a  . Seu raciocínio está ok.
. Seu raciocínio está ok.
Leti Moura escreveu:huum.. eu acho que é mais inifinito, porque ficaria -1/0-, não?
Leti Moura escreveu:obs: c/0- = +infinito, se c>0 ou - infinito, se c<0
Leti Moura escreveu:por que 0+ se tá se aproximando pela esquerda?


Leti Moura escreveu:então a resposta dessa questão seria mesmo +infinito, porque ficaria -1/0-!


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.



