
Nota-se claramente uma indeterminação do tipo "
 ", então eu transformei o produto em um quociente para aplicar L'Hospital e obtive:
", então eu transformei o produto em um quociente para aplicar L'Hospital e obtive: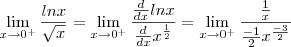
Tipo, eu pensei em multiplicar o númerador e o denominador por
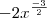 , mas sei lá... Tentei e acho que deu errado.
, mas sei lá... Tentei e acho que deu errado.E empaquei aí... :/ Sei que é meio vergonhoso, mas o cérebro já não está trabalhando tão bem há esta hora. x_x
Bem, qualquer ajuda, eu já agradeço!


![\lim_{x\to0+} \sqrt{x}\ lnx \Rightarrow \lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}} \lim_{x\to0+} \sqrt{x}\ lnx \Rightarrow \lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}}](/latexrender/pictures/afc2594d2a1ab9b3c1fa1be6d1d3af69.png) ,
,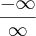 . Assim,
. Assim,![\lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}} = \lim_{x\rightarrow{0}^{+}}\frac{\frac{1}{x}}{\frac{-1}{{x}^{2}}}=-x=0 \lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}} = \lim_{x\rightarrow{0}^{+}}\frac{\frac{1}{x}}{\frac{-1}{{x}^{2}}}=-x=0](/latexrender/pictures/9474b84bba59b158dc6dbce9cf982c6f.png) .
.
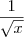 não é
não é  ... E sim
... E sim  , enfim... Depois de um banho, voltei a questão e acho que consegui resolver; se você não tivesse me dado o toque para aquele meu erro, eu demoraria para ter percebido, enfim, ficou assim:
, enfim... Depois de um banho, voltei a questão e acho que consegui resolver; se você não tivesse me dado o toque para aquele meu erro, eu demoraria para ter percebido, enfim, ficou assim:
