 por Jhonata » Seg Mai 28, 2012 23:32
por Jhonata » Seg Mai 28, 2012 23:32
Bem galera, ja vou logo agradecendo, pois até aquele que olha já ajuda muito, enfim, me deparei com o seguinte:

Nota-se claramente uma indeterminação do tipo "

", então eu transformei o produto em um quociente para aplicar L'Hospital e obtive:
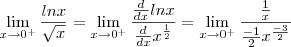
Tipo, eu pensei em multiplicar o númerador e o denominador por
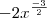
, mas sei lá... Tentei e acho que deu errado.
E empaquei aí... :/ Sei que é meio vergonhoso, mas o cérebro já não está trabalhando tão bem há esta hora. x_x
Bem, qualquer ajuda, eu já agradeço!
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por Russman » Ter Mai 29, 2012 00:00
por Russman » Ter Mai 29, 2012 00:00
Jhonata escreveu:Bem galera, ja vou logo agradecendo, pois até aquele que olha já ajuda muito, enfim, me deparei com o seguinte:

Nota-se claramente uma indeterminação do tipo "

", então eu transformei o produto em um quociente para aplicar L'Hospital e obtive:
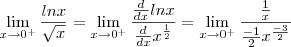
Tipo, eu pensei em multiplicar o númerador e o denominador por
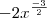
, mas sei lá... Tentei e acho que deu errado.
E empaquei aí... :/ Sei que é meio vergonhoso, mas o cérebro já não está trabalhando tão bem há esta hora. x_x
Bem, qualquer ajuda, eu já agradeço!
Você reescreveu a função de forma errada! O correto é
![\lim_{x\to0+} \sqrt{x}\ lnx \Rightarrow \lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}} \lim_{x\to0+} \sqrt{x}\ lnx \Rightarrow \lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}}](/latexrender/pictures/afc2594d2a1ab9b3c1fa1be6d1d3af69.png)
,
que é uma indeterminação do tipo
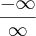
. Assim,
![\lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}} = \lim_{x\rightarrow{0}^{+}}\frac{\frac{1}{x}}{\frac{-1}{{x}^{2}}}=-x=0 \lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}} = \lim_{x\rightarrow{0}^{+}}\frac{\frac{1}{x}}{\frac{-1}{{x}^{2}}}=-x=0](/latexrender/pictures/9474b84bba59b158dc6dbce9cf982c6f.png)
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Jhonata » Ter Mai 29, 2012 00:14
por Jhonata » Ter Mai 29, 2012 00:14
Russman escreveu:Jhonata escreveu:Bem galera, ja vou logo agradecendo, pois até aquele que olha já ajuda muito, enfim, me deparei com o seguinte:

Nota-se claramente uma indeterminação do tipo "

", então eu transformei o produto em um quociente para aplicar L'Hospital e obtive:
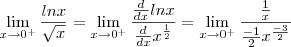
Tipo, eu pensei em multiplicar o númerador e o denominador por
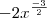
, mas sei lá... Tentei e acho que deu errado.
E empaquei aí... :/ Sei que é meio vergonhoso, mas o cérebro já não está trabalhando tão bem há esta hora. x_x
Bem, qualquer ajuda, eu já agradeço!
Você reescreveu a função de forma errada! O correto é
![\lim_{x\to0+} \sqrt{x}\ lnx \Rightarrow \lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}} \lim_{x\to0+} \sqrt{x}\ lnx \Rightarrow \lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}}](/latexrender/pictures/afc2594d2a1ab9b3c1fa1be6d1d3af69.png)
,
que é uma indeterminação do tipo
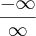
. Assim,
![\lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}} = \lim_{x\rightarrow{0}^{+}}\frac{\frac{1}{x}}{\frac{-1}{{x}^{2}}}=-x=0 \lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}} = \lim_{x\rightarrow{0}^{+}}\frac{\frac{1}{x}}{\frac{-1}{{x}^{2}}}=-x=0](/latexrender/pictures/9474b84bba59b158dc6dbce9cf982c6f.png)
.
Ah, claro!! Que idiotice da minha parte! AHUAHUUA
Por isso não estava conseguindo... Havia esquecido de "notar" isso, bem como eu havia dito... Há esta hora a mente vai parando... huahuhuaa
Mas, então, muito obrigado e tenha uma boa noite!
Abraços!!
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por Jhonata » Ter Mai 29, 2012 01:27
por Jhonata » Ter Mai 29, 2012 01:27
Jhonata escreveu:Russman escreveu:Jhonata escreveu:Bem galera, ja vou logo agradecendo, pois até aquele que olha já ajuda muito, enfim, me deparei com o seguinte:

Nota-se claramente uma indeterminação do tipo "

", então eu transformei o produto em um quociente para aplicar L'Hospital e obtive:
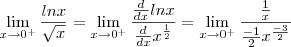
Tipo, eu pensei em multiplicar o númerador e o denominador por
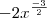
, mas sei lá... Tentei e acho que deu errado.
E empaquei aí... :/ Sei que é meio vergonhoso, mas o cérebro já não está trabalhando tão bem há esta hora. x_x
Bem, qualquer ajuda, eu já agradeço!
Você reescreveu a função de forma errada! O correto é
![\lim_{x\to0+} \sqrt{x}\ lnx \Rightarrow \lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}} \lim_{x\to0+} \sqrt{x}\ lnx \Rightarrow \lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}}](/latexrender/pictures/afc2594d2a1ab9b3c1fa1be6d1d3af69.png)
,
que é uma indeterminação do tipo
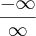
. Assim,
![\lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}} = \lim_{x\rightarrow{0}^{+}}\frac{\frac{1}{x}}{\frac{-1}{{x}^{2}}}=-x=0 \lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}} = \lim_{x\rightarrow{0}^{+}}\frac{\frac{1}{x}}{\frac{-1}{{x}^{2}}}=-x=0](/latexrender/pictures/9474b84bba59b158dc6dbce9cf982c6f.png)
.
Ah, claro!! Que idiotice da minha parte! AHUAHUUA
Por isso não estava conseguindo... Havia esquecido de "notar" isso, bem como eu havia dito... Há esta hora a mente vai parando... huahuhuaa
Mas, então, muito obrigado e tenha uma boa noite!
Abraços!!
Opa, espera aí... Mas acho que também tem algo errado no seu argumento:
A derivada de
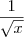
não é

... E sim

, enfim... Depois de um banho, voltei a questão e acho que consegui resolver; se você não tivesse me dado o toque para aquele meu erro, eu demoraria para ter percebido, enfim, ficou assim:


Será que estou certo ou tropecei em algo?
Editado pela última vez por
Jhonata em Ter Mai 29, 2012 01:37, em um total de 1 vez.
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por Russman » Ter Mai 29, 2012 01:37
por Russman » Ter Mai 29, 2012 01:37
Nãaao, tu ta certo! Eu errei na hora de digitar a derivada! Mas, por sorte, daria no mesmo. kk
Só o -2 ali que deveria estar no denominador. Mas tbm, não faz diferença. (:
Editado pela última vez por
Russman em Ter Mai 29, 2012 01:40, em um total de 1 vez.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Jhonata » Ter Mai 29, 2012 01:40
por Jhonata » Ter Mai 29, 2012 01:40
Russman escreveu:Nãaao, tu ta certo! Eu errei na hora de digitar a derivada! Mas, por sorte, daria no mesmo. kk
Bem, a banca da minha faculdade não ia pegar leve com estes nossos erros, mas valeu a pena trabalhar essa questãozinha, que aparentemente é tranquila...
De qualquer forma, muito obrigado mano!!
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por Jhonata » Ter Mai 29, 2012 01:44
por Jhonata » Ter Mai 29, 2012 01:44
Russman escreveu:Nãaao, tu ta certo! Eu errei na hora de digitar a derivada! Mas, por sorte, daria no mesmo. kk
Só o -2 ali que deveria estar no denominador. Mas tbm, não faz diferença. (:
Tipo... Tu tem razão, porquê eu tirei o -2 do denominador? lol
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por Jhonata » Ter Mai 29, 2012 01:44
por Jhonata » Ter Mai 29, 2012 01:44
Jhonata escreveu:Russman escreveu:Nãaao, tu ta certo! Eu errei na hora de digitar a derivada! Mas, por sorte, daria no mesmo. kk
Só o -2 ali que deveria estar no denominador. Mas tbm, não faz diferença. (:
Tipo... Tu tem razão, porquê eu tirei o -2 do denominador? lol
Ahh pô, eu elevei à -1.
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- problema algébrico
por fjf » Dom Out 14, 2012 02:32
- 5 Respostas
- 2525 Exibições
- Última mensagem por DanielFerreira

Dom Out 28, 2012 17:17
Álgebra Elementar
-
- Cálculo algébrico
por Aline Bianca » Qui Jun 24, 2010 22:31
- 2 Respostas
- 1602 Exibições
- Última mensagem por Aline Bianca

Qui Jun 24, 2010 23:16
Álgebra Elementar
-
- Cálculo algébrico 2
por Aline Bianca » Qui Jun 24, 2010 22:50
- 3 Respostas
- 2141 Exibições
- Última mensagem por MarceloFantini

Sex Jun 25, 2010 00:15
Álgebra Elementar
-
- [Cálculo Algébrico] Probleminha simples, ajuda ?
por Gabriel dos Reis » Qui Jul 10, 2014 18:54
- 1 Respostas
- 1305 Exibições
- Última mensagem por young_jedi

Qui Jul 10, 2014 23:27
Álgebra Elementar
-
- [Derivada] Dúvida ao calcular uma derivada...
por dileivas » Ter Mai 01, 2012 09:54
- 2 Respostas
- 2250 Exibições
- Última mensagem por dileivas

Ter Mai 01, 2012 17:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 ", então eu transformei o produto em um quociente para aplicar L'Hospital e obtive:
", então eu transformei o produto em um quociente para aplicar L'Hospital e obtive: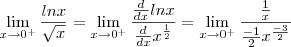
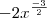 , mas sei lá... Tentei e acho que deu errado.
, mas sei lá... Tentei e acho que deu errado.

![\lim_{x\to0+} \sqrt{x}\ lnx \Rightarrow \lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}} \lim_{x\to0+} \sqrt{x}\ lnx \Rightarrow \lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}}](/latexrender/pictures/afc2594d2a1ab9b3c1fa1be6d1d3af69.png) ,
,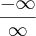 . Assim,
. Assim,![\lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}} = \lim_{x\rightarrow{0}^{+}}\frac{\frac{1}{x}}{\frac{-1}{{x}^{2}}}=-x=0 \lim_{x\rightarrow{0}^{+}}\frac{ln(x)}{\frac{1}{\sqrt[]{x}}} = \lim_{x\rightarrow{0}^{+}}\frac{\frac{1}{x}}{\frac{-1}{{x}^{2}}}=-x=0](/latexrender/pictures/9474b84bba59b158dc6dbce9cf982c6f.png) .
.
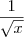 não é
não é  ... E sim
... E sim  , enfim... Depois de um banho, voltei a questão e acho que consegui resolver; se você não tivesse me dado o toque para aquele meu erro, eu demoraria para ter percebido, enfim, ficou assim:
, enfim... Depois de um banho, voltei a questão e acho que consegui resolver; se você não tivesse me dado o toque para aquele meu erro, eu demoraria para ter percebido, enfim, ficou assim:

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
