 por Thiago Ramos » Ter Mai 08, 2012 15:33
por Thiago Ramos » Ter Mai 08, 2012 15:33
Ola Pessoal, teriam como me ajudar na resolucao deste problema Por Favor?
Os Pontos A e B sao opostos um ao outro nas margens de um rio reto que mede 4 Km de largura . O ponto C esta na mesma margem que B , mas a 5 Km , rio abaixo de B. Uma companhia telefonica deseja estender um cabo de A ao ponto P na margem oposta do rio e entao seguir reto ao longo da margem ate o ponto C.Se o Custo por Km do cabo eh de 30% mais caro sob a agua do que em terra, que linha de cabo seria mais barato para a companhia e qual o seu custo????
Determine:
a) O modelamento matematico do problema. (Funcao)
-
Thiago Ramos
-
 por LuizAquino » Ter Mai 08, 2012 17:32
por LuizAquino » Ter Mai 08, 2012 17:32
Thiago Ramos escreveu:Os Pontos A e B sao opostos um ao outro nas margens de um rio reto que mede 4 Km de largura . O ponto C esta na mesma margem que B , mas a 5 Km , rio abaixo de B. Uma companhia telefonica deseja estender um cabo de A ao ponto P na margem oposta do rio e entao seguir reto ao longo da margem ate o ponto C.Se o Custo por Km do cabo eh de 30% mais caro sob a agua do que em terra, que linha de cabo seria mais barato para a companhia e qual o seu custo????
Determine:
a) O modelamento matematico do problema. (Funcao)
Thiago Ramos escreveu:Ola Pessoal, teriam como me ajudar na resolucao deste problema Por Favor?
A figura abaixo ilustra o exercício. Tente resolvê-lo a partir disso. Caso você não consiga terminar, então envie até onde você conseguiu chegar.

- figura.png (3.21 KiB) Exibido 11867 vezes
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Thiago Ramos » Ter Mai 08, 2012 17:36
por Thiago Ramos » Ter Mai 08, 2012 17:36
Eu consegui montar o Grafico deste problema, o que nao estou conseguindo eh achar a funcao. Sei que eh uma funcao do 1grau
-
Thiago Ramos
-
 por joaofonseca » Ter Mai 08, 2012 18:52
por joaofonseca » Ter Mai 08, 2012 18:52
Eu modelei da seguinte forma:
No triangulo [ABP] seja o angulo Â. Seja a amplitude do angulo  em radianos, a variável
x.
Sabemos o comprimento do cateto AB. queremos saber o comprimento do cateto BP em função de
x.

Seja o ponto P, o ponto de "ancoragem", quanto mair for o cateto BP, menor será o trajeto em terra. Logo o trajeto em terra é igual a 5-BP. Ou seja:

Falta agora o trajeto sob água. Na pratica será a hipotenusa do triangulo [ABP]. Um dos catetos tem comprimento fixo de 4, o outro esta definido em função de
x pela expressão
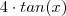
.
Assim a hipotenusa é igual a :

Agora somando as duas partes, temos:
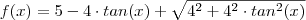
Quando x=0, tan(0)=0. Logo ficamos com

. Quando
x=0,896 rad,

. Por isso temos

O gráfico fica com este aspeto:

- funca#1.jpg (10.48 KiB) Exibido 11859 vezes
Não percebi como determinar o custo?
Editado pela última vez por
joaofonseca em Qua Mai 09, 2012 20:52, em um total de 1 vez.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Thiago Ramos » Ter Mai 08, 2012 19:38
por Thiago Ramos » Ter Mai 08, 2012 19:38
Ola Joao, Obrigado por me ajudar na resolucao da Funcao!.....
Entao quer dizer que Imagem das variaveis envolviodas eh 10?
E para Dominio????
-
Thiago Ramos
-
 por LuizAquino » Ter Mai 08, 2012 20:14
por LuizAquino » Ter Mai 08, 2012 20:14
joaofonseca escreveu:Eu modelei da seguinte forma:
No triangulo [ABP] seja o angulo Â. Seja a amplitude do angulo  em radianos, a variável
x.
Sabemos o comprimento do cateto AB. queremos saber o comprimento do cateto BP em função de
x.

Seja o ponto P, o ponto de "ancoragem", quanto mair for o cateto BP, menor será o trajeto em terra. Logo o trajeto em terra é igual a 5-BP. Ou seja:

Falta agora o trajeto sob água. Na pratica será a hipotenusa do triangulo [ABP]. Um dos catetos tem comprimento fixo de 4, o outro esta definido em função de
x pela expressão
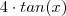
.
Assim a hipotenusa é igual a :

Agora somando as duas partes, temos:
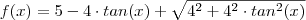
Há uma forma mais direta. Como você já percebeu, ABP é um triângulo retângulo. Sendo BP = x, temos que o comprimento
l do cabo será:

joaofonseca escreveu:Não percebi como determinar o custo?
Suponha que
r seja o custo por km pela terra. Teremos que o custo por km pela água será 1,3
r (ou seja, 130%r). Desse modo, a função custo será:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Thiago Ramos » Ter Mai 08, 2012 20:30
por Thiago Ramos » Ter Mai 08, 2012 20:30
Nao entendi porque deu 1,30 %r! Como vc chegou a isso?
-
Thiago Ramos
-
 por LuizAquino » Ter Mai 08, 2012 20:46
por LuizAquino » Ter Mai 08, 2012 20:46
Thiago Ramos escreveu:Nao entendi porque deu 1,30 %r! Como vc chegou a isso?
Em primeiro lugar, eu não escrevi que era 1,30%r. Eu escrevi que é 1,3r. Ou ainda, que é 130%r.
E em segundo lugar, leia com atenção o enunciado do exercício: "(...)
Se o custo por km do cabo é de 30% mais caro sob a água do que em terra (...)"
Agora responda: o que significa dizer que algo é 30% mais caro do que outra coisa?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Thiago Ramos » Ter Mai 08, 2012 20:49
por Thiago Ramos » Ter Mai 08, 2012 20:49
Muito Obrigado. Consegui compreender bem sua explicacao!
-
Thiago Ramos
-
 por Thiago Ramos » Dom Mai 13, 2012 00:32
por Thiago Ramos » Dom Mai 13, 2012 00:32
Ola Luiz, Nao consegui compreender porque ficou 10 para Y no Grafico que vc mostrou.
E tambem qual e a solucao aproximada analisando o grafico???
-
Thiago Ramos
-
 por LuizAquino » Dom Mai 13, 2012 23:54
por LuizAquino » Dom Mai 13, 2012 23:54
Thiago Ramos escreveu:Ola Luiz, Nao consegui compreender porque ficou 10 para Y no Grafico que vc mostrou.
E tambem qual e a solucao aproximada analisando o grafico???
Até o momento eu não mostrei gráfico algum. Note que quem enviou o gráfico anteriormente foi o participante
joaofonseca.
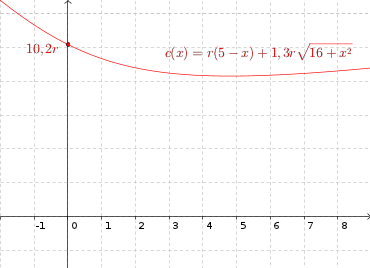
Considerando a função custo dada por

, o seu gráfico está ilustrado na figura abaixo.
- figura.png (11.64 KiB) Exibido 11785 vezes
Agora você mesmo pode analisar o gráfico para determinar aproximadamente para que valor de x temos um mínimo para a função. Basta observar qual seria o ponto "mais baixo" do gráfico.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Thiago Ramos » Seg Mai 14, 2012 00:32
por Thiago Ramos » Seg Mai 14, 2012 00:32
Teve mostrado antes o grafico do modelo do problema. Bem acima como voce pode ver. O grafico da funcao, mas nao o grafico da funcao custo como vc teve mostrado agora.
-
Thiago Ramos
-
 por LuizAquino » Seg Mai 14, 2012 00:48
por LuizAquino » Seg Mai 14, 2012 00:48
Thiago Ramos escreveu:Teve mostrado antes o grafico do modelo do problema. Bem acima como voce pode ver. O grafico da funcao, mas nao o grafico da funcao custo como vc teve mostrado agora.
A imagem que enviei para ilustrar o exercício tipicamente não é chamada de "gráfico". Ela é chamada, por exemplo, de "figura" ou "ilustração".
Quando falamos em gráfico, tipicamente estamos nos referindo ao gráfico da função.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Thiago Ramos » Seg Mai 14, 2012 00:53
por Thiago Ramos » Seg Mai 14, 2012 00:53
Compreendi! Entao isso que eu precisava mesmo. O grafico da Funcao. porque tentei fazer ,mas nao estou conseguindo fazer bem
-
Thiago Ramos
-
 por Thiago Ramos » Seg Mai 14, 2012 00:54
por Thiago Ramos » Seg Mai 14, 2012 00:54
O grafico do modelo da problema(Funcao) e os dominios e imagem das variaveis. Gostaria de confirmar isso!
-
Thiago Ramos
-
 por LuizAquino » Seg Mai 14, 2012 00:57
por LuizAquino » Seg Mai 14, 2012 00:57
Thiago Ramos escreveu:O grafico do modelo da problema(Funcao) e os dominios e imagem das variaveis. Gostaria de confirmar isso!
Podemos fazer melhor. Diga o domínio e a imagem que você encontrou e nós corrigiremos.
Lembre-se da
Regra 1 deste fórum: informar suas tentativas e dificuldades.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Thiago Ramos » Seg Mai 14, 2012 01:01
por Thiago Ramos » Seg Mai 14, 2012 01:01
Entao de acordo com o problema , o dominio que encontreu foi: x pertence aos n. reais tal que x eh maior ou igual a o e menor ou igual a 1,25.
E y pertence aos n. reais tb tal que y eh menor ou igual a 9 e maior ou igual a 6,40
-
Thiago Ramos
-
 por LuizAquino » Seg Mai 14, 2012 10:31
por LuizAquino » Seg Mai 14, 2012 10:31
Thiago Ramos escreveu:Entao de acordo com o problema , o dominio que encontreu foi: x pertence aos n. reais tal que x eh maior ou igual a o e menor ou igual a 1,25.
E y pertence aos n. reais tb tal que y eh menor ou igual a 9 e maior ou igual a 6,40
Está errado.
Considerando a ilustração do problema, temos que o domínio da função

é dado por
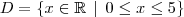
.
Para determinar a imagem dessa função, você precisa determinar o ponto de mínimo e o ponto de máximo no intervalo [0, 5].
Tente continuar a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Nrdm » Ter Mai 15, 2012 17:39
por Nrdm » Ter Mai 15, 2012 17:39
Olá, boa tarde... que mal pergunte, estou acompanhando a resolução deste exercicio, mas minha dúvida permanece, não entendo como encontrar a imagem nesse grafico, pois mesmo que atribua valores ao x na hora de montar não consigo pois no gráfico do custo existem duas icognitas.
Desculpe a ignorancia... estou tentando aprender.
-
Nrdm
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Mai 15, 2012 17:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Civil
- Andamento: cursando
 por LuizAquino » Ter Mai 15, 2012 19:29
por LuizAquino » Ter Mai 15, 2012 19:29
Nrdm escreveu:Olá, boa tarde... que mal pergunte, estou acompanhando a resolução deste exercicio, mas minha dúvida permanece, não entendo como encontrar a imagem nesse grafico, pois mesmo que atribua valores ao x na hora de montar não consigo pois no gráfico do custo existem duas icognitas.
Desculpe a ignorancia... estou tentando aprender.
Vamos imaginar que você tenha que construir o gráfico da função
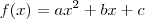
.
Você não conhece os coeficientes a, b e c, mas mesmo assim pode dizer que o formato básico desse gráfico será uma parábola (desde que

).
Você pode dizer isso, pois já fez um estudo a priori sobre funções desse tipo.
Por outro lado, você não estudou funções do tipo que aparece nesse exercício. Entretanto, no caso do exercício temos que
![c(x) = r(5-x) + 1,3r\sqrt{16 + x^2} \implies c(x) = r\left[(5-x) + 1,3\sqrt{16 + x^2}\right] c(x) = r(5-x) + 1,3r\sqrt{16 + x^2} \implies c(x) = r\left[(5-x) + 1,3\sqrt{16 + x^2}\right]](/latexrender/pictures/7f34f78d9a89691858743efc65474b88.png)
Sendo assim, se construirmos o gráfico da função
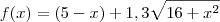
teremos uma versão básica do gráfico de
c, já que
c(
x) =
rf(
x).
Depois de conhecer essa versão básica, podemos imaginar como seria o gráfico no seu formato geral.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Thiago Ramos » Ter Mai 15, 2012 20:03
por Thiago Ramos » Ter Mai 15, 2012 20:03
Oi Luiz.
Estou um pouco confuso.
Entao quer dizer que para y a imagem sera de 0 a 4?
E quanto ao grafico? Qual eh o grafico da funcao que reprrensentao modelo matematico do problema???
-
Thiago Ramos
-
 por LuizAquino » Ter Mai 15, 2012 20:20
por LuizAquino » Ter Mai 15, 2012 20:20
Thiago Ramos escreveu:Estou um pouco confuso.
Entao quer dizer que para y a imagem sera de 0 a 4?
Não.
Para determinar a imagem da função, como eu já disse anteriormente, você precisa determinar o ponto de mínimo e o ponto de máximo no intervalo [0, 5].
Você já estudou sobre o uso de derivadas para calcular o máximo e o mínimo de funções?
Thiago Ramos escreveu:E quanto ao grafico? Qual eh o grafico da funcao que reprrensentao modelo matematico do problema???
Eu já enviei o gráfico em uma mensagem anterior. Você só precisa restringi-lo ao domínio [0, 5], pois na figura apresentada o domínio considerado seria

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Thiago Ramos » Ter Mai 15, 2012 20:29
por Thiago Ramos » Ter Mai 15, 2012 20:29
Nao estudei ponto de minimo e maximo de derivada ainda:(
Entaoo quer dizer que a funcao do do problema eh: F(x) = r(5-x) + 1,3r (raiz)16 + x ao quadrado???
E que a Imagem da Funcao jogando no grafico sera de 0 ate 9?
-
Thiago Ramos
-
 por Thiago Ramos » Ter Mai 15, 2012 20:31
por Thiago Ramos » Ter Mai 15, 2012 20:31
vc poderia me reenviar o grafico novamente?
-
Thiago Ramos
-
 por LuizAquino » Ter Mai 15, 2012 21:08
por LuizAquino » Ter Mai 15, 2012 21:08
Thiago Ramos escreveu:Nao estudei ponto de minimo e maximo de derivada ainda:(
Ok.
Thiago Ramos escreveu:Entaoo quer dizer que a funcao do do problema eh: F(x) = r(5-x) + 1,3r (raiz)16 + x ao quadrado???
Sim, como eu já escrevi anteriormente.
Thiago Ramos escreveu:E que a Imagem da Funcao jogando no grafico sera de 0 ate 9?
De modo geral, não seria isso. A imagem vai mudar conforme seja alterado o valor de r.
Entretanto, como você ainda não estudou a determinação de máximos e mínimos através de derivadas, eu presumo que o exercício deve ser feito pensando em um caso particular. Além disso, que a imagem deve ser determinada de uma forma aproximada, através da análise do gráfico.
Nesse contexto, suponha que r = 1. Temos então a função
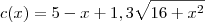
. Agora basta você analisar o gráfico dessa função.
Uma dica: lembre-se que você pode construir esse gráfico usando um programa, como por exemplo o
GeoGebra.
Thiago Ramos escreveu:vc poderia me reenviar o grafico novamente?
Por que enviar novamente? Note que ele já está disponível em uma
mensagem acima!
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Nrdm » Qua Mai 16, 2012 01:18
por Nrdm » Qua Mai 16, 2012 01:18
ok. Agradeço a resposta.
Como também não aprendi maximos e minimos ainda, vou montar o gráfico através da função do custo, atribuindo valores ao x (que seriam de 0 á 5) e para o custo que na verdade pouco importa qual valor eu venha a atribuir, tanto faz (atribuirei 1) bom desta forma acho que entendi, e pela analise do gráfico saberei em qual distancia estará o menor custo. E pelo que pude perceber mas não sei, provavelmente estará no km 5. Ou seja é mais barato passar um cabo direto até o ponto C, que estende-lo metade pela água (ponto P) e + outra metade pela terra até o C.
-
Nrdm
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Mai 15, 2012 17:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Civil
- Andamento: cursando
 por LuizAquino » Qui Mai 17, 2012 00:39
por LuizAquino » Qui Mai 17, 2012 00:39
Nrdm escreveu:Como também não aprendi maximos e minimos ainda, vou montar o gráfico através da função do custo, atribuindo valores ao x (que seriam de 0 á 5) e para o custo que na verdade pouco importa qual valor eu venha a atribuir, tanto faz (atribuirei 1) bom desta forma acho que entendi, e pela analise do gráfico saberei em qual distancia estará o menor custo. E pelo que pude perceber mas não sei, provavelmente estará no km 5. Ou seja é mais barato passar um cabo direto até o ponto C, que estende-lo metade pela água (ponto P) e + outra metade pela terra até o C.
Não está em 5 Km. Está aproximadamente em 4,8 Km. Note que esse é o problema de resolver analisando simplesmente o gráfico: dependendo do tamanho dele você pode ser enganado. A forma mais "segura" de encontrar o mínimo é através das derivadas. Mas você ainda estudará isso.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Nrdm » Qui Mai 17, 2012 09:11
por Nrdm » Qui Mai 17, 2012 09:11
Sim, fiz os calculos, montei o grafico e também cheguei nessa resposta!
Muito obrigada! Ajudou bastante

-
Nrdm
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Mai 15, 2012 17:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo]Alguém me ajuda nessa questão de calculo pfv.
por moeni » Seg Abr 04, 2022 21:54
- 0 Respostas
- 6488 Exibições
- Última mensagem por moeni

Seg Abr 04, 2022 21:54
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4525 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Cálculo Polinômio Interpolador
 por barbara-rabello » Qui Out 22, 2015 20:07
por barbara-rabello » Qui Out 22, 2015 20:07
- 1 Respostas
- 2653 Exibições
- Última mensagem por adauto martins

Sáb Out 24, 2015 11:00
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo] Exercícios de Calculo
por Thomas » Seg Mai 16, 2016 16:39
- 0 Respostas
- 0 Exibições
- Última mensagem por Visitante

Qua Dez 31, 1969 22:00
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5559 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





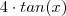 .
.
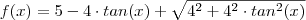
 . Quando x=0,896 rad,
. Quando x=0,896 rad,  . Por isso temos
. Por isso temos 

.




 , o seu gráfico está ilustrado na figura abaixo.
, o seu gráfico está ilustrado na figura abaixo.


 é dado por
é dado por 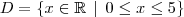 .
.

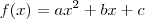 .
. ).
).![c(x) = r(5-x) + 1,3r\sqrt{16 + x^2} \implies c(x) = r\left[(5-x) + 1,3\sqrt{16 + x^2}\right] c(x) = r(5-x) + 1,3r\sqrt{16 + x^2} \implies c(x) = r\left[(5-x) + 1,3\sqrt{16 + x^2}\right]](/latexrender/pictures/7f34f78d9a89691858743efc65474b88.png)
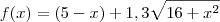 teremos uma versão básica do gráfico de c, já que c(x) = rf(x).
teremos uma versão básica do gráfico de c, já que c(x) = rf(x).
 .
.
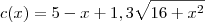 . Agora basta você analisar o gráfico dessa função.
. Agora basta você analisar o gráfico dessa função.




 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: } você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais? } você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?