

Thiago Ramos escreveu:Os Pontos A e B sao opostos um ao outro nas margens de um rio reto que mede 4 Km de largura . O ponto C esta na mesma margem que B , mas a 5 Km , rio abaixo de B. Uma companhia telefonica deseja estender um cabo de A ao ponto P na margem oposta do rio e entao seguir reto ao longo da margem ate o ponto C.Se o Custo por Km do cabo eh de 30% mais caro sob a agua do que em terra, que linha de cabo seria mais barato para a companhia e qual o seu custo????
Determine:
a) O modelamento matematico do problema. (Funcao)
Thiago Ramos escreveu:Ola Pessoal, teriam como me ajudar na resolucao deste problema Por Favor?



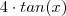 .
.
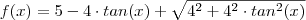
 . Quando x=0,896 rad,
. Quando x=0,896 rad,  . Por isso temos
. Por isso temos 

joaofonseca escreveu:Eu modelei da seguinte forma:
No triangulo [ABP] seja o angulo Â. Seja a amplitude do angulo  em radianos, a variável x.
Sabemos o comprimento do cateto AB. queremos saber o comprimento do cateto BP em função de x.
Seja o ponto P, o ponto de "ancoragem", quanto mair for o cateto BP, menor será o trajeto em terra. Logo o trajeto em terra é igual a 5-BP. Ou seja:
Falta agora o trajeto sob água. Na pratica será a hipotenusa do triangulo [ABP]. Um dos catetos tem comprimento fixo de 4, o outro esta definido em função de x pela expressão.
Assim a hipotenusa é igual a :
Agora somando as duas partes, temos:

joaofonseca escreveu:Não percebi como determinar o custo?


Thiago Ramos escreveu:Nao entendi porque deu 1,30 %r! Como vc chegou a isso?

Thiago Ramos escreveu:Ola Luiz, Nao consegui compreender porque ficou 10 para Y no Grafico que vc mostrou.
E tambem qual e a solucao aproximada analisando o grafico???
 , o seu gráfico está ilustrado na figura abaixo.
, o seu gráfico está ilustrado na figura abaixo.
Thiago Ramos escreveu:Teve mostrado antes o grafico do modelo do problema. Bem acima como voce pode ver. O grafico da funcao, mas nao o grafico da funcao custo como vc teve mostrado agora.

Thiago Ramos escreveu:O grafico do modelo da problema(Funcao) e os dominios e imagem das variaveis. Gostaria de confirmar isso!

Thiago Ramos escreveu:Entao de acordo com o problema , o dominio que encontreu foi: x pertence aos n. reais tal que x eh maior ou igual a o e menor ou igual a 1,25.
E y pertence aos n. reais tb tal que y eh menor ou igual a 9 e maior ou igual a 6,40
 é dado por
é dado por 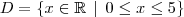 .
.

Nrdm escreveu:Olá, boa tarde... que mal pergunte, estou acompanhando a resolução deste exercicio, mas minha dúvida permanece, não entendo como encontrar a imagem nesse grafico, pois mesmo que atribua valores ao x na hora de montar não consigo pois no gráfico do custo existem duas icognitas.
Desculpe a ignorancia... estou tentando aprender.
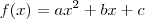 .
. ).
).![c(x) = r(5-x) + 1,3r\sqrt{16 + x^2} \implies c(x) = r\left[(5-x) + 1,3\sqrt{16 + x^2}\right] c(x) = r(5-x) + 1,3r\sqrt{16 + x^2} \implies c(x) = r\left[(5-x) + 1,3\sqrt{16 + x^2}\right]](/latexrender/pictures/7f34f78d9a89691858743efc65474b88.png)
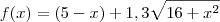 teremos uma versão básica do gráfico de c, já que c(x) = rf(x).
teremos uma versão básica do gráfico de c, já que c(x) = rf(x).
Thiago Ramos escreveu:Estou um pouco confuso.
Entao quer dizer que para y a imagem sera de 0 a 4?
Thiago Ramos escreveu:E quanto ao grafico? Qual eh o grafico da funcao que reprrensentao modelo matematico do problema???
 .
.
Thiago Ramos escreveu:Nao estudei ponto de minimo e maximo de derivada ainda:(
Thiago Ramos escreveu:Entaoo quer dizer que a funcao do do problema eh: F(x) = r(5-x) + 1,3r (raiz)16 + x ao quadrado???
Thiago Ramos escreveu:E que a Imagem da Funcao jogando no grafico sera de 0 ate 9?
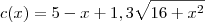 . Agora basta você analisar o gráfico dessa função.
. Agora basta você analisar o gráfico dessa função.Thiago Ramos escreveu:vc poderia me reenviar o grafico novamente?


Nrdm escreveu:Como também não aprendi maximos e minimos ainda, vou montar o gráfico através da função do custo, atribuindo valores ao x (que seriam de 0 á 5) e para o custo que na verdade pouco importa qual valor eu venha a atribuir, tanto faz (atribuirei 1) bom desta forma acho que entendi, e pela analise do gráfico saberei em qual distancia estará o menor custo. E pelo que pude perceber mas não sei, provavelmente estará no km 5. Ou seja é mais barato passar um cabo direto até o ponto C, que estende-lo metade pela água (ponto P) e + outra metade pela terra até o C.



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

