 por LuizCarlos » Ter Abr 24, 2012 13:08
por LuizCarlos » Ter Abr 24, 2012 13:08
Olá, estou resolvendo exercícios sobre quadriláteros!
Mas essa questão não estou entendendo:
6) Sabendo que AP e BP são bissetrizes, determine x nos casos:
Não estou entendo essa questão de bissetrizes, minha dúvida é a seguinte, no caso dessas duas questões a e b, as bissetrizes AP e BP dividem os ângulos  e B em dois ângulos congruentes, isso é uma pergunta, pois meu teclado está sem acentuação.
Tentei resolver dessa forma, mas não creio que esteja certo!
Determinei o valor do ângulo BPA como sendo x. Então:
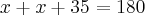
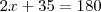
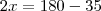

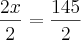
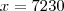
setenta e dois graus e 30 minutos
Mas creio que esteja errado, não estou conseguindo entender essas questões para poder resolver. Ajuda fazendo favor!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por DanielFerreira » Ter Abr 24, 2012 20:00
por DanielFerreira » Ter Abr 24, 2012 20:00
a)
Considere o ângulo B valendo 2k;
Sabemos que  vale 130° (65°+ 65°);
A soma dos ângulos internos vale 360°, sabemos que  vale 130° e D = 80°, então:
A + B + C + D = 360°
130° + 2k + x + 80° = 360°
2k + x = 150°
Pelo Teorema do ângulo externo temos:
x + 35° = 65° + k
k - x = - 30°
Resolvendo o sistema encontrará o valor de "x".
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Ter Abr 24, 2012 20:10
por DanielFerreira » Ter Abr 24, 2012 20:10
b)
Considerando o ângulo A valendo 2a, temos: BÂP = a;
Considerando o ângulo B valendo 2b, temos: ABP = b.
Soma dos ângulos internos do triângulo: a + b + x = 180°
Soma dos ângulos internos do quadrilátero: 2a + 2b + 100° + x = 360°
I)
a + b + x = 180°
a + b = 180° - x
II)
2a + 2b + 100º + x = 360°
2(a + b) = 360° - x - 100
2(a + b) = 260° - x
2(180° - x) = 260° - x
360° - 2x = 260° - x
360° - 260° = 2x - x
x = 100°
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por LuizCarlos » Ter Abr 24, 2012 22:11
por LuizCarlos » Ter Abr 24, 2012 22:11
danjr5 escreveu:a)
Considere o ângulo B valendo 2k;
Sabemos que  vale 130° (65°+ 65°);
A soma dos ângulos internos vale 360°, sabemos que  vale 130° e D = 80°, então:
A + B + C + D = 360°
130° + 2k + x + 80° = 360°
2k + x = 150°
Pelo Teorema do ângulo externo temos:
x + 35° = 65° + k
k - x = - 30°
Resolvendo o sistema encontrará o valor de "x".
Olá amigo danjr5, perfeita sua explicação, consegui entender perfeitamente! muito obrigado, você é um ótimo professor! continue assim, ajudando quem precisa! Deus ti abençoe, sou muito grato pela ajuda!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por LuizCarlos » Ter Abr 24, 2012 22:12
por LuizCarlos » Ter Abr 24, 2012 22:12
danjr5 escreveu:b)
Considerando o ângulo A valendo 2a, temos: BÂP = a;
Considerando o ângulo B valendo 2b, temos: ABP = b.
Soma dos ângulos internos do triângulo: a + b + x = 180°
Soma dos ângulos internos do quadrilátero: 2a + 2b + 100° + x = 360°
I)
a + b + x = 180°
a + b = 180° - x
II)
2a + 2b + 100º + x = 360°
2(a + b) = 360° - x - 100
2(a + b) = 260° - x
2(180° - x) = 260° - x
360° - 2x = 260° - x
360° - 260° = 2x - x
x = 100°
Olá amigo danjr5, perfeita sua explicação, consegui entender perfeitamente! muito obrigado, você é um ótimo professor! continue assim, ajudando quem precisa! Deus ti abençoe, sou muito grato pela ajuda! você está de parabéns!

-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por DanielFerreira » Qui Abr 26, 2012 20:18
por DanielFerreira » Qui Abr 26, 2012 20:18
Valeu pelo elogio LuizCarlos!
Ainda não sou professor, falta bastante tempo. Rssrs
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- quadriláteros
 por fttofolo » Sex Jan 28, 2011 21:33
por fttofolo » Sex Jan 28, 2011 21:33
- 1 Respostas
- 2697 Exibições
- Última mensagem por VtinxD

Sex Jan 28, 2011 23:04
Geometria Plana
-
- Quadrilateros convexos
 por laisv11 » Sex Mai 15, 2009 16:19
por laisv11 » Sex Mai 15, 2009 16:19
- 2 Respostas
- 3762 Exibições
- Última mensagem por admin

Sáb Mai 16, 2009 00:53
Geometria Plana
-
- Quadriláteros notáveis
 por Jean Cigari » Qua Jun 22, 2011 11:26
por Jean Cigari » Qua Jun 22, 2011 11:26
- 2 Respostas
- 14914 Exibições
- Última mensagem por Jean Cigari

Qua Jun 22, 2011 22:30
Geometria Plana
-
- circunferência e quadriláteros
 por fttofolo » Qua Fev 15, 2012 14:12
por fttofolo » Qua Fev 15, 2012 14:12
- 4 Respostas
- 8076 Exibições
- Última mensagem por fttofolo

Ter Fev 28, 2012 21:35
Geometria Plana
-
- [QUADRILÁTEROS]ÁREAS
 por anabrizola » Seg Ago 05, 2013 22:31
por anabrizola » Seg Ago 05, 2013 22:31
- 0 Respostas
- 1533 Exibições
- Última mensagem por anabrizola

Seg Ago 05, 2013 22:31
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
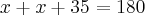
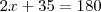
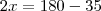

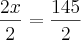
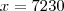




![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.