Mas essa questão não estou entendendo:
6) Sabendo que AP e BP são bissetrizes, determine x nos casos:
Não estou entendo essa questão de bissetrizes, minha dúvida é a seguinte, no caso dessas duas questões a e b, as bissetrizes AP e BP dividem os ângulos  e B em dois ângulos congruentes, isso é uma pergunta, pois meu teclado está sem acentuação.
Tentei resolver dessa forma, mas não creio que esteja certo!
Determinei o valor do ângulo BPA como sendo x. Então:
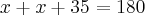
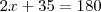
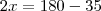

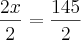
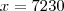
setenta e dois graus e 30 minutos
Mas creio que esteja errado, não estou conseguindo entender essas questões para poder resolver. Ajuda fazendo favor!





 , avisa que eu resolvo.
, avisa que eu resolvo.

