por Feliperpr » Ter Abr 24, 2012 21:14
por Feliperpr » Ter Abr 24, 2012 21:14
Considere o cilindro C = {(x, y, z), x²+y² =2, 0 < z < 2}. Utilizando o teorema de Stokes calcule o ?uxo do campo de vetores F(x, y, z) = (x, y, ?2 z) através de C no sentido da normal exterior.
Se utilizarmos Stokes, obtemos que o rotacional dá zero. Logo a integral seria zero?
Se fizer pelo cálculo do fluxo, temos como parametrização
![r(\Theta, z)= (\sqrt[2]{2} *cos \Theta, \sqrt[2]{2}sen\Theta, z) r(\Theta, z)= (\sqrt[2]{2} *cos \Theta, \sqrt[2]{2}sen\Theta, z)](/latexrender/pictures/1c9b2f73145982f5194b2b3251475870.png)
Necessitamos calcular dr/dz X dr/ do?
Está certo isso?
-
Feliperpr
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Abr 21, 2012 15:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Russman » Ter Abr 24, 2012 21:24
por Russman » Ter Abr 24, 2012 21:24
Com o teorema de Stokes se calcula o fluxo do rotacional de F, não de F. Ainda, o teorema de Stokes expõe uma forma alternativa de calcular trabalho de deslocamento sobre caminhos fechado.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Feliperpr » Ter Abr 24, 2012 21:28
por Feliperpr » Ter Abr 24, 2012 21:28
Mas então o enunciado está estranho, né?
Pq ele pede pra calcular o fluxo do campo e não do rotacional do campo! Por isso que tentei utilizar calculando diretamente!
-
Feliperpr
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Abr 21, 2012 15:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Russman » Ter Abr 24, 2012 21:30
por Russman » Ter Abr 24, 2012 21:30
É, ta incoerente com a teoria! Eu acredito que a melhor saída é usar o Teorema da Divergência de Gauss.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Feliperpr » Ter Abr 24, 2012 21:34
por Feliperpr » Ter Abr 24, 2012 21:34
Obrigado! Vou fazer aqui! E tem que abrir ainda..pq a superfície não é fechada! Mas obrigado!

-
Feliperpr
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Abr 21, 2012 15:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Russman » Ter Abr 24, 2012 21:38
por Russman » Ter Abr 24, 2012 21:38
Aí depende do problema. O enunciado não dá muita idéia se a superficie é fechada ou não. A meu entendemento, o cilindro é uma superfície fechada. Por isso eu sigeri o Teorema da Divergência. Mas se for só o fluxo através do tronco do cilindro calcula pela definição mesmo de fluxo. (;
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Feliperpr » Ter Abr 24, 2012 21:44
por Feliperpr » Ter Abr 24, 2012 21:44
Eu acredito que a superfície seria fechada neste caso se z fosse maior e igual a 0 e menor e igual a 2.
Supondo que não seja fechada, a parametrização que escolhi está certa, né? E na hora de cálcular o produto vetorial é daquele jeito mesmo?
Pq geralmente sobram 2 parametros na parametrização somente! Só que o z só está ligado a terceira coordenada sem relação com as outras duas! =S
-
Feliperpr
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Abr 21, 2012 15:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Russman » Ter Abr 24, 2012 21:54
por Russman » Ter Abr 24, 2012 21:54
Feliperpr escreveu:Eu acredito que a superfície seria fechada neste caso se z fosse maior e igual a 0 e menor e igual a 2.
Supondo que não seja fechada, a parametrização que escolhi está certa, né? E na hora de cálcular o produto vetorial é daquele jeito mesmo?
Pq geralmente sobram 2 parametros na parametrização somente! Só que o z só está ligado a terceira coordenada sem relação com as outras duas! =S
Supondo a superfície aberta.
Você conhece o teorema a seguir?
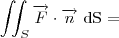

"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Feliperpr » Ter Abr 24, 2012 21:57
por Feliperpr » Ter Abr 24, 2012 21:57
Que eu me lembre não vi nada nesse formato! :/
-
Feliperpr
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Abr 21, 2012 15:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Russman » Ter Abr 24, 2012 22:00
por Russman » Ter Abr 24, 2012 22:00
Comoo você calcularia então o fluxo através do cilindro aberto? Qual fórmula?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Feliperpr » Ter Abr 24, 2012 22:04
por Feliperpr » Ter Abr 24, 2012 22:04
Desculpa se eu estiver errado...mas tentaria calcular usando a primeira fórmula até antes do igual! Que é a formula geral do fluxo, não? =S
-
Feliperpr
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Abr 21, 2012 15:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Russman » Ter Abr 24, 2012 22:10
por Russman » Ter Abr 24, 2012 22:10
É maais dificil usando a definição! Se você utilizar aquele teorema que eu postei fica mais fácil. Ele consiste em calcular o fluxo através do cilindro aberto usando o fluxo através de uma "sombra" do mesmo, que é o plano R.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Feliperpr » Ter Abr 24, 2012 22:18
por Feliperpr » Ter Abr 24, 2012 22:18
Vou procurar! Muito obrigado!

-
Feliperpr
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Abr 21, 2012 15:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo Vetorial - Parametrização] - Reta
por anselmojr97 » Dom Mar 20, 2016 01:25
- 0 Respostas
- 2514 Exibições
- Última mensagem por anselmojr97

Dom Mar 20, 2016 01:25
Equações
-
- Parametrização de superfície
por AllanGeoffroy » Ter Mar 05, 2013 11:56
- 0 Respostas
- 896 Exibições
- Última mensagem por AllanGeoffroy

Ter Mar 05, 2013 11:56
Cálculo: Limites, Derivadas e Integrais
-
- PARAMETRIZAÇÃO DE CURVAS
por sasuyanli » Sáb Out 26, 2013 12:14
- 1 Respostas
- 3915 Exibições
- Última mensagem por e8group

Dom Nov 03, 2013 14:31
Cálculo: Limites, Derivadas e Integrais
-
- [CURVAS] CÁLC II - Trajetórias e Parametrização
por inkz » Ter Nov 20, 2012 01:12
- 6 Respostas
- 4343 Exibições
- Última mensagem por inkz

Ter Nov 20, 2012 11:53
Cálculo: Limites, Derivadas e Integrais
-
- [CURVAS] Parametrização de elipse e vetores tangentes
por inkz » Ter Nov 20, 2012 04:43
- 2 Respostas
- 2762 Exibições
- Última mensagem por inkz

Qua Nov 21, 2012 03:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![r(\Theta, z)= (\sqrt[2]{2} *cos \Theta, \sqrt[2]{2}sen\Theta, z) r(\Theta, z)= (\sqrt[2]{2} *cos \Theta, \sqrt[2]{2}sen\Theta, z)](/latexrender/pictures/1c9b2f73145982f5194b2b3251475870.png)

![r(\Theta, z)= (\sqrt[2]{2} *cos \Theta, \sqrt[2]{2}sen\Theta, z) r(\Theta, z)= (\sqrt[2]{2} *cos \Theta, \sqrt[2]{2}sen\Theta, z)](/latexrender/pictures/1c9b2f73145982f5194b2b3251475870.png)