Gente, eu entrei na 4ª lista da Universidade entao perdi muita materia, agora to com dificuldade... To começando a pegar o jeito, mas esse problema eu não consigo!
O problema é o seguinte
Prove pela definição formal de limites o seguinte limite:

Bom... eu consegui pensar em diversas coisas mas nenhuma delas ajuda, e nenhuma delas é certeza de que são pensamentos corretos.
Eu pensei na propriedade de que se f(x) e g(x) são contínuas, eu sei que f(x)+g(x) é uma função continua. entao posso separar em dois limites que eu tenho que provar.
Teria que provar que
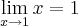 e Depois teria que provar que
e Depois teria que provar que 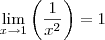
Certo. O primeiro é facil. não precisa de nada. Agora o segundo é Complicado. não consigo fazer nada... =/
Se eu tento criar um
 pra tentar exibir um
pra tentar exibir um  eu simplesmente não consigo.
eu simplesmente não consigo. Obrigado pela atenção


 existe um
existe um  tal que
tal que 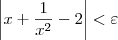 sempre que
sempre que 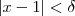 .
.
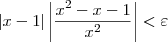
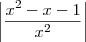 , ou seja, determinar uma constante
, ou seja, determinar uma constante  .
.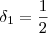 .
. e
e  para 1/2 < x < 3/2, temos que
para 1/2 < x < 3/2, temos que 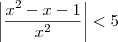
 . Nesse caso, bastava tomar
. Nesse caso, bastava tomar 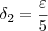 .
. . Isto é, devemos tomar
. Isto é, devemos tomar  .
.
 ?
?
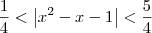
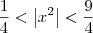
 .
.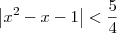 e
e 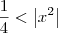 , então temos que:
, então temos que: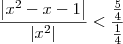
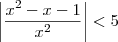
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.