 por jmbraganca » Qui Mar 22, 2012 20:41
por jmbraganca » Qui Mar 22, 2012 20:41
Então galera, beleza? To com uma dúvida que já revirei um tanto de livros, um tanto de cadernos, revirei o google e não achei a resposta de como proceder. Provavelmente eu não estou procurando direito, mas será que vocês podem me ajudar?
Eu estou com essa fórmula abaixo':
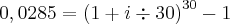
O que eu fiz foi passar o 1 'somando' para o outro lado da igualdade e depois passei o 30 que estava dividindo o i para o outro lado da igualdade, só que multiplicando. Ficou assim:
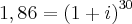
De qualquer forma, acho que errei passando o 30 e também não sei o que fazer com o 'i' e com o expoente lá em cima. Alguém por favor pode me dar uma luz? Estou desesperado e quebrando a cabeça para resolver este exercício, mas não consigo!
-
jmbraganca
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Mar 22, 2012 20:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por nietzsche » Qui Mar 22, 2012 21:05
por nietzsche » Qui Mar 22, 2012 21:05
O i denota a unidade imaginária?
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por joaofonseca » Qui Mar 22, 2012 21:09
por joaofonseca » Qui Mar 22, 2012 21:09
Parto do principio que i não é a unidade imaginaria, até porque se assim fosse não fazia sentido encontrar o valor de i.
A expressão que foi colocada não é uma equação exponencial, pois a variável não está como expoente.É uma equação "normal" com uma potência.Logo resolve-se como normalmente se resolvem as equações polinomiais de 1º,2º ou 3º grau.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por jmbraganca » Qui Mar 22, 2012 21:19
por jmbraganca » Qui Mar 22, 2012 21:19
O i é uma incógnita. Consegui resolver, eu passei o -1 para o outro lado somando, depois tirei a raiz 30ª dos dois lados e depois passei o +1 para o outro lado subtraindo e depois multipliquei pelo 30 e achei a resposta.
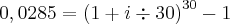
Passando aquele -1 para o lado esquerdo da igualdade:
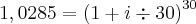
Tirando a raiz dos dois lados:
![\sqrt[30]{1,0285} = \sqrt[30]{{\left(1 + i\div30 \right)}^{30}} \sqrt[30]{1,0285} = \sqrt[30]{{\left(1 + i\div30 \right)}^{30}}](/latexrender/pictures/87b8bb7f29ed392e297a25c4564ff034.png)
Resultado:

Após isso, passar esse 1 para o lado esquerdo da igualdade, ficando assim:
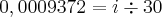
Agora o 30 que está dividindo passará multiplicando e teremos o resultado de i:
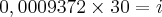
Valor de i:
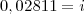
Prontinho, de acordo com meu gabarito está certinho ^^
Valeuzão galera!
-
jmbraganca
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Mar 22, 2012 20:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por nietzsche » Qui Mar 22, 2012 21:28
por nietzsche » Qui Mar 22, 2012 21:28
É verdade, é que não li o título da pergunta. Tinha pensado em algo como provar que o lado esquerdo pode ser igual ao lado direito.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação exponencial???
por azheng » Sáb Nov 21, 2009 19:47
- 0 Respostas
- 1620 Exibições
- Última mensagem por azheng

Sáb Nov 21, 2009 19:47
Álgebra Elementar
-
- Equação Exponencial
por Adriana Baldussi » Seg Nov 23, 2009 14:41
- 3 Respostas
- 2825 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 17:07
Álgebra Elementar
-
- Equação Exponencial
por LeonardoSantos » Ter Fev 16, 2010 14:11
- 1 Respostas
- 2819 Exibições
- Última mensagem por Douglasm

Ter Fev 16, 2010 15:46
Funções
-
- Equação exponencial
por cristina » Sex Jun 04, 2010 20:19
- 1 Respostas
- 2237 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 00:27
Sistemas de Equações
-
- Equação exponencial
por nan_henrique » Sáb Jul 10, 2010 13:00
- 1 Respostas
- 2184 Exibições
- Última mensagem por Douglasm

Sáb Jul 10, 2010 13:12
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
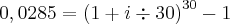
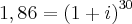




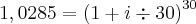
![\sqrt[30]{1,0285} = \sqrt[30]{{\left(1 + i\div30 \right)}^{30}} \sqrt[30]{1,0285} = \sqrt[30]{{\left(1 + i\div30 \right)}^{30}}](/latexrender/pictures/87b8bb7f29ed392e297a25c4564ff034.png)

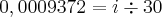
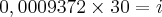
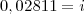


 , avisa que eu resolvo.
, avisa que eu resolvo.

