
Meu livro traz duas relações sobre setor circular:
Relacionando raio(r) e comprimento(l=AB):
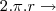
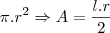
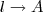
Relacionando raio (r) e ângulo:




Com isso é possível calcular a área lateral de um cone por meio da primeira relação (considerando que o raio do setor terá o valor da geratriz do cone (g):
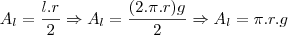
Ele também chega numa fórmula que calcula o ângulo do setor:

Tentei demonstrar essa fórmula. Igualei as duas relações, chegando à
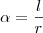
Então, chamei r de g.
Primeira dúvida: O modo como demonstrei é o correto?
Segunda dúvida: Como resolver o exercício abaixo:
A área lateral de um cone de revolução é
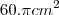 . Desenvolvendo a superfície lateral, tem-se um setor circular de raio 10cm. A medida do ângulo central desse setor, em radianos, é:
. Desenvolvendo a superfície lateral, tem-se um setor circular de raio 10cm. A medida do ângulo central desse setor, em radianos, é:Gabarito:
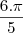
Tentei jogar na fórmula que calcula o ângulo do setor, mas cheguei em
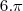 , o que é absurdo.
, o que é absurdo.

 e a área
e a área  , basta montar uma regra de três simples com o comprimento
, basta montar uma regra de três simples com o comprimento  e área
e área  , e queremos relacionar com
, e queremos relacionar com 
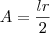 e
e 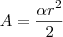 ), você obteve que em qualquer setor circular de raio
), você obteve que em qualquer setor circular de raio 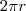 , sendo
, sendo 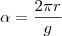 . Com isso você chega na fórmula que desejava.
. Com isso você chega na fórmula que desejava. cm². Desenvolvendo a superfície lateral, tem-se um setor circular de raio 10 cm. A medida do ângulo central desse setor, em radianos, é:
cm². Desenvolvendo a superfície lateral, tem-se um setor circular de raio 10 cm. A medida do ângulo central desse setor, em radianos, é: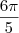







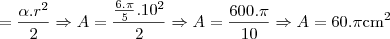

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.