por Arkanus Darondra » Qua Fev 01, 2012 22:07
por Arkanus Darondra » Qua Fev 01, 2012 22:07
Explicando as relaçõesRelacionando raio(r) e comprimento(l=AB):Se em uma circunferência completa o comprimento é

e a área

, basta montar uma regra de três simples com o comprimento

e área
 Relacionando raio (r) e ângulo:
Relacionando raio (r) e ângulo:Mesma lógica de cima, considerando que em uma circunferência completa o ângulo é de 360º, ou seja,

, e queremos relacionar com

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Qui Fev 02, 2012 02:28
por LuizAquino » Qui Fev 02, 2012 02:28
Arkanus Darondra escreveu:Ele também chega numa fórmula que calcula o ângulo do setor:
Tentei demonstrar essa fórmula. Igualei as duas relações, chegando à
Então, chamei r de g.
Primeira dúvida: O modo como demonstrei é o correto?
Em resumo: Ao igualar as duas relações (isto é,
e
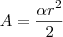
), você obteve que em qualquer setor circular de raio
r, ângulo central

e comprimento
l, é válida a relação
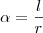
. Isso está correto.
No caso do cone circular reto, o setor circular que representa a sua área lateral tem raio medindo
g e comprimento medindo
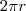
, sendo
r o raio da base (vide a figura abaixo). Vamos dizer que o seu ângulo central seja

. Substituindo essas informações na relação que você encontrou, temos que
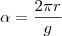
. Com isso você chega na fórmula que desejava.

- cone-circular-reto.png (11.07 KiB) Exibido 5737 vezes
Arkanus Darondra escreveu:Segunda dúvida: Como resolver o exercício abaixo:
A área lateral de um cone de revolução é

cm². Desenvolvendo a superfície lateral, tem-se um setor circular de raio 10 cm. A medida do ângulo central desse setor, em radianos, é:
Gabarito:
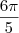
Da primeira informação do problema, temos que:

Da segunda informação do problema, temos que:

Dessas duas informações, concluímos que:

Por fim, usando a fórmula para o ângulo central:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Arkanus Darondra » Qui Fev 02, 2012 11:37
por Arkanus Darondra » Qui Fev 02, 2012 11:37
Valeu!

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Arkanus Darondra » Sáb Fev 04, 2012 12:39
por Arkanus Darondra » Sáb Fev 04, 2012 12:39
Surgiu outra dúvida: Qual a relação entre área lateral de um cone com o seu setor circular? São iguais?
O exercício diz que a área lateral é de

Partindo da segunda relação:
A
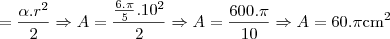
Creio que isso que tenha me confundido no exercício acima, pois troquei comprimento pela área, chegando, erroneamente, à

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Dom Fev 05, 2012 00:08
por LuizAquino » Dom Fev 05, 2012 00:08
Arkanus Darondra escreveu:Surgiu outra dúvida: Qual a relação entre área lateral de um cone com o seu setor circular? São iguais?
Não é que um cone circular reto "tenha" um setor circular.
O que acontece é que a sua área lateral ao ser "desenrolada" da base faz surgir um setor circular.
Falando de forma mais formal, ao planificarmos um cone circular reto nós obtemos um círculo (proveniente da base) e um setor circular (proveniente da lateral).
Nesse contexto, verificamos que a área lateral de um cone circular reto é igual a área do setor circular proveniente de sua planificação.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Arkanus Darondra » Dom Fev 05, 2012 09:20
por Arkanus Darondra » Dom Fev 05, 2012 09:20
LuizAquino escreveu:Falando de forma mais formal, ao planificarmos um cone circular reto nós obtemos um círculo (proveniente da base) e um setor circular (proveniente da lateral).
Nesse contexto, verificamos que a área lateral de um cone circular reto é igual a área do setor circular proveniente de sua planificação.
Certo. Valeu novamente!

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Setor circular
 por DanielFerreira » Sex Mar 04, 2011 11:08
por DanielFerreira » Sex Mar 04, 2011 11:08
- 1 Respostas
- 3964 Exibições
- Última mensagem por LuizAquino

Sex Mar 04, 2011 12:08
Geometria Plana
-
- area do setor circular
 por stanley tiago » Seg Mai 02, 2011 16:35
por stanley tiago » Seg Mai 02, 2011 16:35
- 3 Respostas
- 2451 Exibições
- Última mensagem por FilipeCaceres

Seg Mai 02, 2011 19:51
Geometria Analítica
-
- Permutação circular
por anfran1 » Dom Nov 17, 2013 10:53
- 0 Respostas
- 1084 Exibições
- Última mensagem por anfran1

Dom Nov 17, 2013 10:53
Análise Combinatória
-
- pista circular
por adauto martins » Seg Set 29, 2014 15:45
- 1 Respostas
- 1172 Exibições
- Última mensagem por adauto martins

Sex Jul 22, 2016 17:04
Cálculo: Limites, Derivadas e Integrais
-
- Calculo circular
por lucastrmendes » Sex Mai 08, 2015 16:07
- 0 Respostas
- 2249 Exibições
- Última mensagem por lucastrmendes

Sex Mai 08, 2015 16:07
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

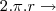
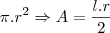
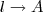




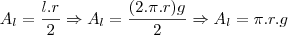

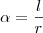
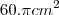 . Desenvolvendo a superfície lateral, tem-se um setor circular de raio 10cm. A medida do ângulo central desse setor, em radianos, é:
. Desenvolvendo a superfície lateral, tem-se um setor circular de raio 10cm. A medida do ângulo central desse setor, em radianos, é: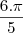
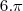 , o que é absurdo.
, o que é absurdo.

 e a área
e a área  , basta montar uma regra de três simples com o comprimento
, basta montar uma regra de três simples com o comprimento  e área
e área  , e queremos relacionar com
, e queremos relacionar com 
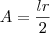 e
e 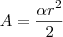 ), você obteve que em qualquer setor circular de raio
), você obteve que em qualquer setor circular de raio 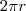 , sendo
, sendo 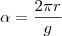 . Com isso você chega na fórmula que desejava.
. Com isso você chega na fórmula que desejava. cm². Desenvolvendo a superfície lateral, tem-se um setor circular de raio 10 cm. A medida do ângulo central desse setor, em radianos, é:
cm². Desenvolvendo a superfície lateral, tem-se um setor circular de raio 10 cm. A medida do ângulo central desse setor, em radianos, é: