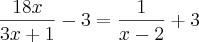
Fiquei um dia inteiro resolvendo essa equação, eu consegui após muito tempo a resposta 11/9, que está correta.
Porém a forma que eu utilizei para resolve-lá foi que me motivou a buscar uma opinião.
Eu passei os elementos para o lado esquerdo e utilizei um principio de proporcionalidade que deixou a equação no seguinte formato:
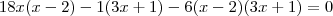
Como pode ser visto, multipliquei os termos antecedentes com os termos consequentes. Mas ai vai a minha dúvida:
O 6 está para 1, por isso não adicionei esse termo na hora de multiplicar com os termos adjacentes. Mas se o 6 estivesse para 2x + 1 por exemplo? A equação ficaria da seguinte forma:
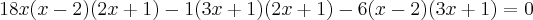
Veja que agora estou multiplicando o 2x + 1 pelos termos adjacentes. Isso eu faria por dedução, mas encontrei alguns exercícios resolvidos não fazem desta maneira. Poderiam me dizer o que está errado no seu raciocínio?
Desde já agradeço.




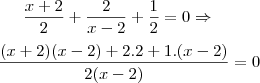


 ...
...
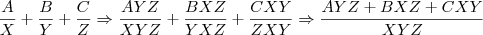

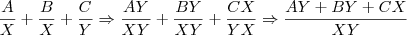 ...
...

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.