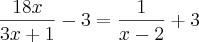
Fiquei um dia inteiro resolvendo essa equação, eu consegui após muito tempo a resposta 11/9, que está correta.
Porém a forma que eu utilizei para resolve-lá foi que me motivou a buscar uma opinião.
Eu passei os elementos para o lado esquerdo e utilizei um principio de proporcionalidade que deixou a equação no seguinte formato:
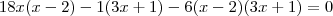
Como pode ser visto, multipliquei os termos antecedentes com os termos consequentes. Mas ai vai a minha dúvida:
O 6 está para 1, por isso não adicionei esse termo na hora de multiplicar com os termos adjacentes. Mas se o 6 estivesse para 2x + 1 por exemplo? A equação ficaria da seguinte forma:
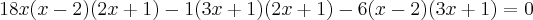
Veja que agora estou multiplicando o 2x + 1 pelos termos adjacentes. Isso eu faria por dedução, mas encontrei alguns exercícios resolvidos não fazem desta maneira. Poderiam me dizer o que está errado no seu raciocínio?
Desde já agradeço.




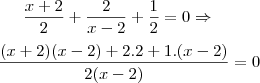


 ...
...
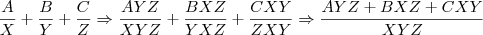

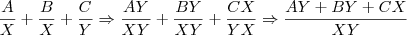 ...
...


 .
.
 :
: