Terei que apresentá-lo resolvido semana que vem e já tem uns 5 dias que to quebrando a cabeça...
O problema é o seguinte:
Provar que se
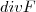 e
e 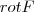 são nulos, então
são nulos, então 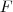 é um campo de quadrado inverso.
é um campo de quadrado inverso.Eu acredito que há um erro no enunciado, que o que realmente vale é a recíproca, pois no caso do enunciado acima podemos ter
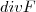 e
e 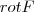 nulos, porém
nulos, porém 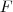 um campo constante qualquer e não necessariamente (como indica) um campo de quadrado inverso :
um campo constante qualquer e não necessariamente (como indica) um campo de quadrado inverso :Provar que se
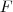 é um campo de quadrado inverso, então
é um campo de quadrado inverso, então 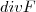 e
e 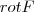 são nulos.
são nulos.Já tentei de várias formas, até mesmo usando o Teorema de Gauss (Teorema da divergência) e o teorema de Stokes, mas não sei como proceder.
Se o enunciado estiver correto, eu acredito que o problema seja simples de resolver mas queria que me ajudassem a encontrar a melhor resposta...
Desde já agradece quem se disponibilizar.


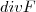 e
e  ,
,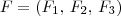 , temos que:
, temos que: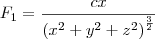
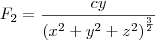
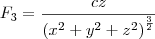
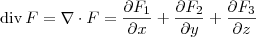
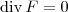 .
.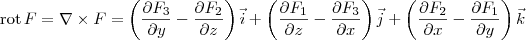
 .
.
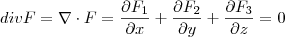
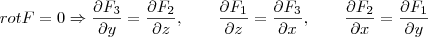
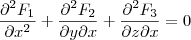
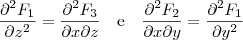
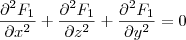
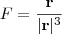 .
.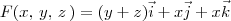 . Note que
. Note que 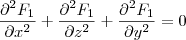
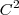 .
.
 .
.



