por GabyRitter » Ter Mai 19, 2009 22:43
Olá...
Estou encontrando dificuldade em encontrar o número de raízes de um polinômio!
Já tentei tornar de várias formas, mas elas não tem dado certo, creio que estou com alguma informação trocada!
Se alguém souber relmente como fazer agradeço!
-
GabyRitter
- Novo Usuário
-
- Mensagens: 7
- Registrado em: Dom Mai 17, 2009 19:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
por GabyRitter » Ter Mai 19, 2009 22:44
,,,
-
GabyRitter
- Novo Usuário
-
- Mensagens: 7
- Registrado em: Dom Mai 17, 2009 19:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
por Cleyson007 » Qua Mai 20, 2009 09:50
Bom dia Gaby, tudo bem?
Por favor coloque a questão no fórum
Talvez possa ajudá-la, ou algum outro usuário deste fórum, ok?
Um abraço.
Até mais.
-
Cleyson007
- Colaborador Voluntário
-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
por GabyRitter » Qua Mai 20, 2009 22:58
A questão é a seguinte:
- Dado o polinômio p(x) = 4x(3) - 4x(2) - 4x
Obs: o que esta entre parenteses ao lado do x é a potência a qual o x está elevado.
a. P2(x) = p(x) + 6. Quantas raizes o polinômio P2(x) possui?
Encontrei os divisores de 6 e os testei, mas não encontrei nunhuma raiz real, mas na resposta do exercício diz que tem UMA raiz.
-
GabyRitter
- Novo Usuário
-
- Mensagens: 7
- Registrado em: Dom Mai 17, 2009 19:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
por Cleyson007 » Sex Mai 22, 2009 08:49
Bom dia Gaby, tudo bem?
Entendi que você está querendo o seguinte:
Dado o polinômio p(x) = 4x³ - 4x² - 4x
P(x)² = 4x³ - 4x² - 4x + 6.
Quantas raizes o polinômio P(x)² possui?
Ele possui 3 raízes, pois seu grau é 3.
Tente colocar a questão usando o "Editor de Fórmulas", ok?
Bons estudos.
Um abraço
-
Cleyson007
- Colaborador Voluntário
-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
por Molina » Sáb Mai 23, 2009 00:29
Cleyson007 escreveu:Bom dia Gaby, tudo bem?
Entendi que você está querendo o seguinte:
Dado o polinômio p(x) = 4x³ - 4x² - 4x
P(x)² = 4x³ - 4x² - 4x + 6.
Quantas raizes o polinômio P(x)² possui?
Ele possui 3 raízes, pois seu grau é 3.
Tente colocar a questão usando o "Editor de Fórmulas", ok?
Bons estudos.
Um abraço
Olá, Cleyson.
Acho que não é
P(x)².
Ela chamou de P2(x) outro polinômio contendo o p(x),
ou seja,
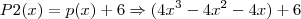
Ok? Pelo menos foi isso que eu entendi.
Abraços,
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-
Molina
- Colaborador Moderador - Professor
-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- raizes de polinomios de grau 3
por theSinister » Seg Mai 09, 2011 17:58
- 9 Respostas
- 5462 Exibições
- Última mensagem por theSinister
Seg Mai 09, 2011 21:35
Álgebra Elementar
-
- Polinômios - Raízes complexas
por Malorientado » Dom Out 07, 2012 15:45
- 3 Respostas
- 1982 Exibições
- Última mensagem por MarceloFantini
Dom Out 07, 2012 20:21
Polinômios
-
- Polinômios" Multiplicidade de raizes de polinômio
por Rose » Sex Set 21, 2012 18:42
- 3 Respostas
- 2307 Exibições
- Última mensagem por young_jedi
Sáb Set 22, 2012 10:08
Polinômios
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8111 Exibições
- Última mensagem por adauto martins
Sáb Ago 27, 2016 16:11
Números Complexos
-
- [Radiciação] Raízes dentro de raízes
por mottasky » Ter Set 13, 2011 22:00
- 2 Respostas
- 2568 Exibições
- Última mensagem por mottasky
Qui Set 15, 2011 15:52
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {
} e B = {
}, então o número de elementos A
B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
