Tenho duas dúvidas com a prova de
 implica
implica  (isto é, que se f é par, então sua derivada f' é ímpar).
(isto é, que se f é par, então sua derivada f' é ímpar).Lembrando que:
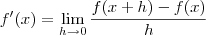
A prova começa assim:
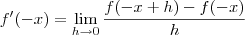
Mas aqui eu já tenho a primeira dúvida: se em
 o
o  é na verdade algo como
é na verdade algo como  , como eu posso fazer
, como eu posso fazer 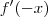 substituindo
substituindo  por
por  na expressão original, mas sem tocar no
na expressão original, mas sem tocar no  ? Parece-me que
? Parece-me que  passaria a ser
passaria a ser  , mas então deixaria de ser
, mas então deixaria de ser  .
.Engolindo isso, a prova continua. Terei uma segunda dúvida. Continuando, há esses passos:
![f'(-x)=\lim_{h\rightarrow0}\frac{f[-(x-h)]-f(-x)}{h}=\lim_{h\rightarrow0}\frac{f(x-h)-f(x)}{h} f'(-x)=\lim_{h\rightarrow0}\frac{f[-(x-h)]-f(-x)}{h}=\lim_{h\rightarrow0}\frac{f(x-h)-f(x)}{h}](/latexrender/pictures/8d2c19b80d26726cdf903e23ee4559fb.png)
Aqui ok: como a função é par, os
 ficaram
ficaram  acima. E a seguir introduz-se um sinal de menos dentro e fora do limite. Ok também:
acima. E a seguir introduz-se um sinal de menos dentro e fora do limite. Ok também: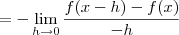
E nesse ponto toma-se
 e faz-se:
e faz-se:
Isso é
 , concluindo a prova. Mas - segunda dúvida - me incomoda que, no símbolo de limite, a substituição seja
, concluindo a prova. Mas - segunda dúvida - me incomoda que, no símbolo de limite, a substituição seja  em vez de
em vez de  . Isso não deveria fazer diferença? Não ficaria
. Isso não deveria fazer diferença? Não ficaria 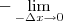 ali?
ali?Agradeço a quem puder me ajudar.
P. S.: tirei essa demonstração do livro (e-book) de respostas do Cálculo vol. 6 (James Stewart).
Atualizado: já posso ver que tanto faz colocar
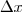 ou
ou  no limite, porque se um tende a zero, o outro também. Essa é a explicação da segunda dúvida, certo? A primeira dúvida permanece. Pensando aqui...
no limite, porque se um tende a zero, o outro também. Essa é a explicação da segunda dúvida, certo? A primeira dúvida permanece. Pensando aqui...


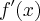 é :
é :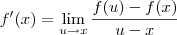

 (que é o mesmo que
(que é o mesmo que  ). Note que quando
). Note que quando  , temos que
, temos que 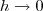 . Sendo assim, podemos reescrever a expressão anterior como:
. Sendo assim, podemos reescrever a expressão anterior como:
 . Por isso não há problema algum escrever que:
. Por isso não há problema algum escrever que:

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.