eu tenho um jeito. mas não tenho certeza nenhuma se é o correto...
em fim...
calcule
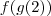
obteremos
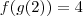
duas maneiras para prosseguir:
Para qual numero eu devo avaliar a f de modo que resulte no numero 4 ? (obs: não estou falando da variável x, estou falando do numero a ser avaliado f(?) )
como
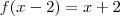
voce observa que para x = 2 voce obtém o 4 esperado!
e qual numero voce está calculando a f para esse x = 2 ?
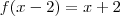
para x = 2
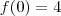
se
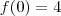
e
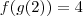
imagino eu que
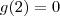
outro jeito é o que eu tenho mais receio de dizer aqui... não sou professor nem nada, entao adimito. pode estar meio errado!
vamos manipular a função
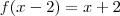
se eu avalia-la nos pontos x = z + 2, estou compondo a função de modo a obter uma função de 1 variavel normal:
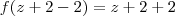
dai
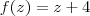
para qual valor eu obtenho a imagem 4 ?
z = 0
entao se
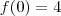
e
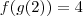
...... =))
 e
e  , calcule o valor de
, calcule o valor de 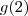 .
.
 e
e  , calcule o valor de
, calcule o valor de 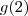 .
.
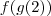
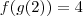
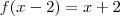
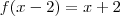
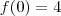
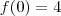 e
e 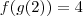 imagino eu que
imagino eu que 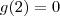
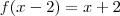
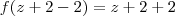
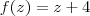
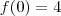 e
e 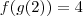 ...... =))
...... =))





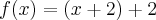
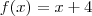
 basta substituir em
basta substituir em  e igualar a
e igualar a 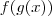
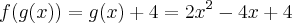
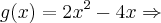 temos
temos 


...

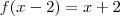 , podemos concluir que
, podemos concluir que  . Daí,
. Daí,  o que implica
o que implica 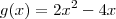 .
.

