 por Richard Oliveira » Seg Nov 07, 2011 16:17
por Richard Oliveira » Seg Nov 07, 2011 16:17
Olá, tenho dificuldades para resolver questões sobre função, por isso estou dedicando todo o tempo livre para aprender sobre esse assunto. Já li muitas coisas a respeito, porém, sinto falta de exemplos e resoluções para entender as mesmas. Por esse mesmo motivo aproveito o espaço que o fórum oferece para aprender com aqueles que já entendem o assunto e não pensam duas vezes antes de ajudar. A todos, agradeço pela paciência com que tem sobre os que tem dificuldade. Segue a questão:
Se

e

, calcule o valor de
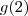
.
-
Richard Oliveira
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Nov 04, 2011 16:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por TheoFerraz » Seg Nov 07, 2011 16:34
por TheoFerraz » Seg Nov 07, 2011 16:34
eu tenho um jeito. mas não tenho certeza nenhuma se é o correto...
em fim...
calcule
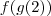
obteremos
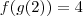
duas maneiras para prosseguir:
Para qual numero eu devo avaliar a f de modo que resulte no numero 4 ? (obs: não estou falando da variável x, estou falando do numero a ser avaliado f(?) )
como
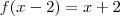
voce observa que para x = 2 voce obtém o 4 esperado!
e qual numero voce está calculando a f para esse x = 2 ?
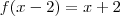
para x = 2
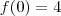
se
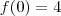
e
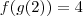
imagino eu que
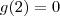
outro jeito é o que eu tenho mais receio de dizer aqui... não sou professor nem nada, entao adimito. pode estar meio errado!
vamos manipular a função
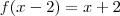
se eu avalia-la nos pontos x = z + 2, estou compondo a função de modo a obter uma função de 1 variavel normal:
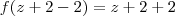
dai
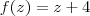
para qual valor eu obtenho a imagem 4 ?
z = 0
entao se
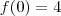
e
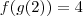
...... =))
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por Richard Oliveira » Seg Nov 07, 2011 17:43
por Richard Oliveira » Seg Nov 07, 2011 17:43
Realmente sua resposta foi igual a do gabarito, g(2)= 0. No primeiro modo eu entendi bem como foi feito. Pela lógica ficou bem fácil achar a resposta. O segundo modo eu acho que consegui entender também, bem interessante. Uma outra pessoa me ensinou de outro jeito, porém eu não entendi o que foi feito no começo:
Dados:


Primeiro encontrar o f(x):
Quando



aplique:
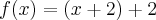
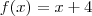
Agora para encontrar

basta substituir em

e igualar a
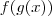
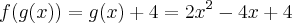
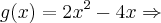
temos

Agora aplique:

Alguém me explica o que foi feito no começo da resolução?
-
Richard Oliveira
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Nov 04, 2011 16:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por TheoFerraz » Seg Nov 07, 2011 17:55
por TheoFerraz » Seg Nov 07, 2011 17:55
Na verdade, o que foi feito não foi diferente do que eu fiz na segunda explicação!
Veja a minha segunda explicação. eu substitui aonde tinha x por k +2 de modo que eu pudesse exibir o x "dentro" da f
foi exatamente o que ele fez, na verdade, mas ele não mudou de variável de x para k
observe a passagem
Quando
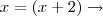
...
é exatamente o que eu fiz quando disse que x = k + 2
só que eu pra não confundir eu usei uma nova letra...
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por MarceloFantini » Seg Nov 07, 2011 18:46
por MarceloFantini » Seg Nov 07, 2011 18:46
Se
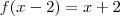
, podemos concluir que

. Daí,

o que implica
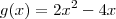
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Richard Oliveira » Seg Nov 07, 2011 21:05
por Richard Oliveira » Seg Nov 07, 2011 21:05
Agradeço a vocês pelas respostas, me ajudou bastante a entender. Entendi as resoluções, não é tão difícil quanto parece. Obrigado pela paciência.
-
Richard Oliveira
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Nov 04, 2011 16:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- como resolver esse tipo de conta?
por LuizCarlos » Seg Jul 11, 2011 00:43
- 11 Respostas
- 6159 Exibições
- Última mensagem por LuizCarlos

Ter Jul 12, 2011 20:00
Sistemas de Equações
-
- Equações diferenciais: ordem, tipo e grau
 por luanavsr » Qui Set 05, 2013 14:56
por luanavsr » Qui Set 05, 2013 14:56
- 0 Respostas
- 1328 Exibições
- Última mensagem por luanavsr

Qui Set 05, 2013 14:56
Cálculo: Limites, Derivadas e Integrais
-
- Dificuldade em resolver o exercicio nº 2
por Catriane Moreira » Sáb Nov 20, 2010 23:01
- 1 Respostas
- 2166 Exibições
- Última mensagem por alexandre32100

Seg Nov 22, 2010 14:42
Matemática Financeira
-
- dificuldade em resolver matriz inversa
por oliveiracld » Qua Mar 09, 2011 00:38
- 4 Respostas
- 3853 Exibições
- Última mensagem por LuizAquino

Qua Mar 09, 2011 20:19
Matrizes e Determinantes
-
- Dificuldade ao resolver uma Integral Racinal
por rubenesantos » Seg Mai 02, 2011 22:38
- 1 Respostas
- 1823 Exibições
- Última mensagem por LuizAquino

Seg Mai 02, 2011 22:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  , calcule o valor de
, calcule o valor de 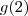 .
.
 e
e  , calcule o valor de
, calcule o valor de 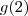 .
.
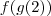
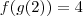
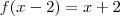
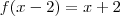
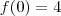
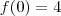 e
e 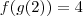 imagino eu que
imagino eu que 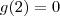
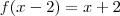
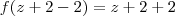
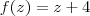
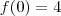 e
e 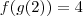 ...... =))
...... =))





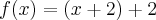
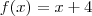
 basta substituir em
basta substituir em  e igualar a
e igualar a 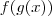
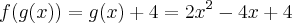
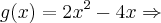 temos
temos 


...

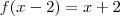 , podemos concluir que
, podemos concluir que  . Daí,
. Daí,  o que implica
o que implica 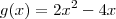 .
.

