Encontre todos os valores de x nos quais a reta tangente a curva dada satisfaz a propriedade enunciada.
 ;passa pela origem.
;passa pela origem.
 ;passa pela origem.
;passa pela origem.
 o coeficiente angular.
o coeficiente angular.
 um pto q a reta passa.
um pto q a reta passa.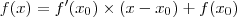


TheoFerraz escreveu:Assim,
Como escrevemos uma equação de reta ?
Nós precisamos de um ponto que ela passa e um coeficiente angular (obs, se isso não estiver claro avise-me.)
Vamos chamar deo coeficiente angular.
uma reta seria dada pela equação:
sendoum pto q a reta passa.
No caso de uma reta tangente, nós podemos interpretar o 'm' como a derivada da função naquele ponto, entao ficaria.
a ideia é, construa essa equação usando a função dada e verifique se a reta passa pela origem, em outras palavras se
(Obs, como eu não estou com mto tempo eu respondi meio acoxambrado, esperando que voce soubesse já diversas coisas dessas, o por que desse coeficiente angular, essa derivada, ou melhor, o porque dessa equação geral pra retas existe e é compreensível, o mesmo pra derivada ser o coeficiente angular no caso duma tg. se isso não estiver claro eu explico.)

elizandro escreveu:TheoFerraz escreveu:Assim,
Como escrevemos uma equação de reta ?
Nós precisamos de um ponto que ela passa e um coeficiente angular (obs, se isso não estiver claro avise-me.)
Vamos chamar deo coeficiente angular.
uma reta seria dada pela equação:
sendoum pto q a reta passa.
No caso de uma reta tangente, nós podemos interpretar o 'm' como a derivada da função naquele ponto, entao ficaria.
a ideia é, construa essa equação usando a função dada e verifique se a reta passa pela origem, em outras palavras se
(Obs, como eu não estou com mto tempo eu respondi meio acoxambrado, esperando que voce soubesse já diversas coisas dessas, o por que desse coeficiente angular, essa derivada, ou melhor, o porque dessa equação geral pra retas existe e é compreensível, o mesmo pra derivada ser o coeficiente angular no caso duma tg. se isso não estiver claro eu explico.)

elizandro escreveu:c puder fazer o calculo pra mim que eu tentei fazer mas n fecha o resultado q é -2
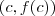 é dada por:
é dada por: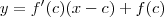
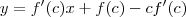

 , precisamos resolver:
, precisamos resolver:
 nos quais a reta tangente ao gráfico de f passa pela origem.
nos quais a reta tangente ao gráfico de f passa pela origem.
LuizAquino escreveu:elizandro escreveu:c puder fazer o calculo pra mim que eu tentei fazer mas n fecha o resultado q é -2
Você já sabe que a reta tangente ao gráfico de f no pontoé dada por:
Ou ainda, podemos escrever:
Para que essa reta passe pela origem, deve ocorrer:
Ou seja, já que, precisamos resolver:
Sendo assim, basta resolver essa equação para descobrir todos os pontosnos quais a reta tangente ao gráfico de f passa pela origem.
Foi uma equação como essa que você resolveu? Qual foi o seu desenvolvimento?

elizandro escreveu:não fecha com a resposta que ta no livro -2

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes