Olá, alguém poderia me ajudar com essas questões?^^
1-Seja u =(2,3), e as bases B1={(1,2),(-1,3)},B2={(2,1),(-2,1)}
a) Escreva o vetor u nas bases B1 e B2.
b) Escreva o vetor coordenada de u nas duas bases.
Qual a diferença dessas duas questões?
sei que para escrever o vetor coordenada de u nas bases é só usar combinação linear.
tipo:
u=a(1,2)+b(-1,3)
(2,3)=a(1,2)+b(-1,3)
e u=a(2,1)+b(-2,1)
(2,3)=a(2,1)+b(-2,1)
Qual diferença do que pede em a para b?
a outra questão é:
2- Mostre que B={(1,0),(i,0),(0,1),(0,1),(0,i)} é base do espaço vetorial dos pares ordenados dos números complexos sobre o corpo dos complexos A={(u,v)/u,v E C}.
sei que a idéia é saber se B é li e se B gera V.
Mas como fica fazendo isso com números complexos.
Só faltam essas questões para terminar a lista que a professora pediu.
Alguém poderia me ajudar por favor?:)


 . Escrever o vetor
. Escrever o vetor  nessa base significa determinar as constantes
nessa base significa determinar as constantes  e
e  tais que
tais que 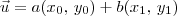 . O par
. O par  é chamado de vetor coordenada de
é chamado de vetor coordenada de 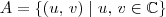 é escrevendo
é escrevendo 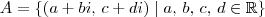 .
.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.