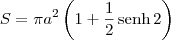por maykonnunes » Qui Set 15, 2011 23:54
por maykonnunes » Qui Set 15, 2011 23:54
Encontre a área da superfície formada oela rotação, ao rdor do eixo x, do gráfico da função
![f(x)= a. cosh\frac{x}{a} ,/ x\epsilon[0,a] f(x)= a. cosh\frac{x}{a} ,/ x\epsilon[0,a]](/latexrender/pictures/dee6474fa65c3b4a6c39e54d8c8531a7.png)
-
maykonnunes
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 02:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por LuizAquino » Sáb Set 17, 2011 20:27
por LuizAquino » Sáb Set 17, 2011 20:27
maykonnunes escreveu:Encontre a área da superfície formada pela rotação, ao redor do eixo x, do gráfico da função
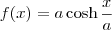
,
![x\in [0,a] x\in [0,a]](/latexrender/pictures/a2e0a7db6b58ff7d7b743cc581bf12b3.png)
Dos conhecimentos de Cálculo, sabemos que a área da superfície obtida será dada por
![S = \int_{0}^{a} 2\pi f(x) \sqrt{1 + [f^\prime(x)]^2}\,dx S = \int_{0}^{a} 2\pi f(x) \sqrt{1 + [f^\prime(x)]^2}\,dx](/latexrender/pictures/fd3416f8ca23636de00b3734a78844c3.png)
Por definição, o
cosseno hiperbólico (representado por
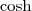
) é definido como:
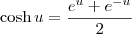
Sendo assim, temos que:
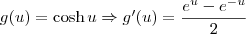
Note que podemos escrever:
![\sqrt{1 + [g^\prime(u)]^2} = \sqrt{1 + \left(\frac{e^u - e^{-u}}{2}\right)^2} \sqrt{1 + [g^\prime(u)]^2} = \sqrt{1 + \left(\frac{e^u - e^{-u}}{2}\right)^2}](/latexrender/pictures/feede8311f2f939785db2f327f3070e9.png)

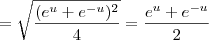
Considerando essas informações, tente terminar o exercício.
ObservaçãoPor definição, o
seno hiperbólico (representado por

) é definido como:
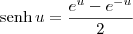
Desse maneira, temos que:
(i)
![[\cosh u]^\prime = \textrm{senh}\, u [\cosh u]^\prime = \textrm{senh}\, u](/latexrender/pictures/f22768b9f29e98207b507f554673cf07.png)
(ii)
![[\textrm{senh}\, u]^\prime = \cosh u [\textrm{senh}\, u]^\prime = \cosh u](/latexrender/pictures/53536557cb2a98b2f13ab397339f2452.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Faby » Qua Set 21, 2011 17:56
por Faby » Qua Set 21, 2011 17:56
...estou tentando continuar a resolução, fiz mudançã de variável, mas não consigo encontrar a v onde dv é (e^x/a + e^-x/a)/2 dx
-
Faby
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Faby » Sex Set 23, 2011 14:11
por Faby » Sex Set 23, 2011 14:11
...cheguei ao seguinte resultado:
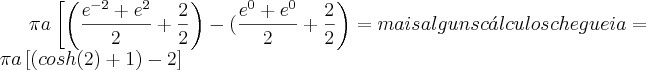
será que acertei??
-
Faby
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Sáb Set 24, 2011 00:39
por LuizAquino » Sáb Set 24, 2011 00:39
Considerando as informações que postei anteriormente e usando a Regra da Cadeia, note que:
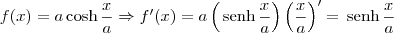
Além disso, também temos que:

Portanto, precisamos apenas calcular a integral:
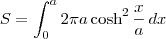
Utilizando as definições apresentadas anteriormente, é fácil verificar que é válida a identidade
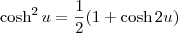
.
Podemos então reescrever o integrando como:

Agora basta resolver essas duas integrais. Vale lembrar que na segunda delas podemos aplicar a substituição

e

.
No final, o resultado será:
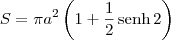
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Área - Na próxima figura ABCD é um quadrilátero de área 200
 por marguiene » Sex Out 10, 2014 10:22
por marguiene » Sex Out 10, 2014 10:22
- 0 Respostas
- 2129 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:22
Geometria Plana
-
- Área - Na figura abaixo ABCD é um retângulo de área 11 cm².
 por marguiene » Sex Out 10, 2014 10:35
por marguiene » Sex Out 10, 2014 10:35
- 0 Respostas
- 2899 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:35
Geometria Plana
-
- como calcular o volume da figura
 por eliane e rodrigo » Seg Ago 23, 2010 22:33
por eliane e rodrigo » Seg Ago 23, 2010 22:33
- 2 Respostas
- 2103 Exibições
- Última mensagem por eliane e rodrigo

Ter Ago 24, 2010 16:45
Geometria Espacial
-
- Calcular lado de uma figura formada por uma recta paralela
por LBT » Dom Dez 05, 2010 17:22
- 2 Respostas
- 2002 Exibições
- Última mensagem por LBT

Seg Dez 06, 2010 05:35
Geometria Analítica
-
- Área - Na figura abaixo D, E, F, G são pontos médios. Determ
 por marguiene » Sex Out 10, 2014 10:00
por marguiene » Sex Out 10, 2014 10:00
- 0 Respostas
- 2438 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:00
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)= a. cosh\frac{x}{a} ,/ x\epsilon[0,a] f(x)= a. cosh\frac{x}{a} ,/ x\epsilon[0,a]](/latexrender/pictures/dee6474fa65c3b4a6c39e54d8c8531a7.png)


![f(x)= a. cosh\frac{x}{a} ,/ x\epsilon[0,a] f(x)= a. cosh\frac{x}{a} ,/ x\epsilon[0,a]](/latexrender/pictures/dee6474fa65c3b4a6c39e54d8c8531a7.png)

,
![S = \int_{0}^{a} 2\pi f(x) \sqrt{1 + [f^\prime(x)]^2}\,dx S = \int_{0}^{a} 2\pi f(x) \sqrt{1 + [f^\prime(x)]^2}\,dx](/latexrender/pictures/fd3416f8ca23636de00b3734a78844c3.png)
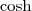 ) é definido como:
) é definido como: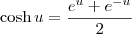
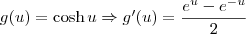
![\sqrt{1 + [g^\prime(u)]^2} = \sqrt{1 + \left(\frac{e^u - e^{-u}}{2}\right)^2} \sqrt{1 + [g^\prime(u)]^2} = \sqrt{1 + \left(\frac{e^u - e^{-u}}{2}\right)^2}](/latexrender/pictures/feede8311f2f939785db2f327f3070e9.png)

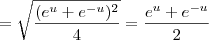
 ) é definido como:
) é definido como: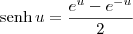
![[\cosh u]^\prime = \textrm{senh}\, u [\cosh u]^\prime = \textrm{senh}\, u](/latexrender/pictures/f22768b9f29e98207b507f554673cf07.png)
![[\textrm{senh}\, u]^\prime = \cosh u [\textrm{senh}\, u]^\prime = \cosh u](/latexrender/pictures/53536557cb2a98b2f13ab397339f2452.png)


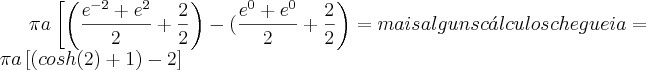

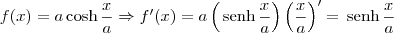

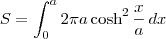
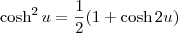 .
.
 e
e  .
.