 por beel » Ter Set 06, 2011 13:10
por beel » Ter Set 06, 2011 13:10
lim [ 2 + (cos x)/x ]
quando x tende ao infinito
Eu teria que transformar o cosseno em seno pra aplicar o limite fundamental trigonométrico?
E se for, como se faz isso?
Obs: o editor de formulas nao estava abrindo, desculpa escrever desse jeito
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Neperiano » Ter Set 06, 2011 14:45
por Neperiano » Ter Set 06, 2011 14:45
Ola
Sen = 1/cosseno
Então Cosseno = 1/seno
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por beel » Ter Set 06, 2011 15:23
por beel » Ter Set 06, 2011 15:23
Nao seria, cos = 1 - sen?
Enfim, nao entendi de qualquer forma, o que eu faço?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Ter Set 06, 2011 18:13
por MarceloFantini » Ter Set 06, 2011 18:13
A relação fundamental é
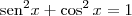
. Esclareça, por favor:
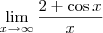
ou
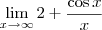
?
Neperiano, novamente, por favor tome cuidado pois sua afirmação não faz sentido e está equivocada.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por beel » Qui Set 08, 2011 14:53
por beel » Qui Set 08, 2011 14:53
A segunda opção( x dividindo apenas o cos(x) )
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Qui Set 08, 2011 18:54
por LuizAquino » Qui Set 08, 2011 18:54
isanobile,
Você já estudou o
Teorema do Sanduíche (ou Teorema do Confronto)?
Dos conhecimentos de trigonometria, sabemos que:
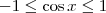
Considerando x não nulo e positivo, podemos multiplicar toda essa inequação por 1/x e ela não se altera:
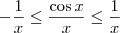
Veja que
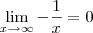
e
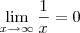
. Portanto, pelo Teorema do Sanduíche, segue que
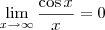
.
Isso significa que
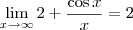
.
ObservaçãoO colega Fantini enviou sua mensagem às 18:48, enquanto eu ainda editava a minha mensagem (que foi enviada às 18:54). Portanto, desculpem a duplicidade na resposta.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Sex Set 09, 2011 13:16
por beel » Sex Set 09, 2011 13:16
Já estudei isso sim, consegui entender, obrigada pela explicação detalhada.
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Seno e cosseno
por KleinIll » Qua Out 31, 2012 15:01
- 2 Respostas
- 2665 Exibições
- Última mensagem por e8group

Qua Out 31, 2012 20:34
Cálculo: Limites, Derivadas e Integrais
-
- Limite: Cosseno(x) e Seno(x) com X tendendo a infinito
por lucasguilherme2 » Qui Mai 24, 2012 11:49
- 3 Respostas
- 44430 Exibições
- Última mensagem por LuizAquino

Ter Mai 29, 2012 11:54
Cálculo: Limites, Derivadas e Integrais
-
- Cosseno
por karen » Ter Nov 27, 2012 13:17
- 1 Respostas
- 1557 Exibições
- Última mensagem por MarceloFantini

Ter Nov 27, 2012 19:24
Trigonometria
-
- Cosseno (FUVEST)
 por Ananda » Sex Mar 14, 2008 22:37
por Ananda » Sex Mar 14, 2008 22:37
- 4 Respostas
- 6399 Exibições
- Última mensagem por Ananda

Seg Mar 17, 2008 17:28
Geometria Espacial
-
- Função Cosseno
por DanielFerreira » Qui Jul 30, 2009 17:41
- 1 Respostas
- 2868 Exibições
- Última mensagem por Felipe Schucman

Qui Jul 30, 2009 18:01
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





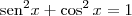 . Esclareça, por favor:
. Esclareça, por favor: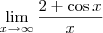 ou
ou 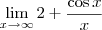 ?
?



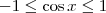
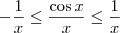
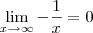 e
e 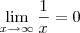 . Portanto, pelo Teorema do Sanduíche, segue que
. Portanto, pelo Teorema do Sanduíche, segue que 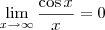 .
.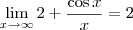 .
.



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.