 por beel » Ter Set 06, 2011 13:10
por beel » Ter Set 06, 2011 13:10
lim [ 2 + (cos x)/x ]
quando x tende ao infinito
Eu teria que transformar o cosseno em seno pra aplicar o limite fundamental trigonométrico?
E se for, como se faz isso?
Obs: o editor de formulas nao estava abrindo, desculpa escrever desse jeito
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Neperiano » Ter Set 06, 2011 14:45
por Neperiano » Ter Set 06, 2011 14:45
Ola
Sen = 1/cosseno
Então Cosseno = 1/seno
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por beel » Ter Set 06, 2011 15:23
por beel » Ter Set 06, 2011 15:23
Nao seria, cos = 1 - sen?
Enfim, nao entendi de qualquer forma, o que eu faço?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Ter Set 06, 2011 18:13
por MarceloFantini » Ter Set 06, 2011 18:13
A relação fundamental é
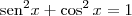
. Esclareça, por favor:
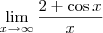
ou
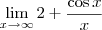
?
Neperiano, novamente, por favor tome cuidado pois sua afirmação não faz sentido e está equivocada.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por beel » Qui Set 08, 2011 14:53
por beel » Qui Set 08, 2011 14:53
A segunda opção( x dividindo apenas o cos(x) )
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Qui Set 08, 2011 18:54
por LuizAquino » Qui Set 08, 2011 18:54
isanobile,
Você já estudou o
Teorema do Sanduíche (ou Teorema do Confronto)?
Dos conhecimentos de trigonometria, sabemos que:
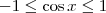
Considerando x não nulo e positivo, podemos multiplicar toda essa inequação por 1/x e ela não se altera:
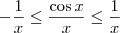
Veja que
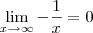
e
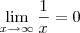
. Portanto, pelo Teorema do Sanduíche, segue que
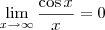
.
Isso significa que
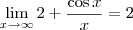
.
ObservaçãoO colega Fantini enviou sua mensagem às 18:48, enquanto eu ainda editava a minha mensagem (que foi enviada às 18:54). Portanto, desculpem a duplicidade na resposta.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Sex Set 09, 2011 13:16
por beel » Sex Set 09, 2011 13:16
Já estudei isso sim, consegui entender, obrigada pela explicação detalhada.
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Seno e cosseno
por KleinIll » Qua Out 31, 2012 15:01
- 2 Respostas
- 2672 Exibições
- Última mensagem por e8group

Qua Out 31, 2012 20:34
Cálculo: Limites, Derivadas e Integrais
-
- Limite: Cosseno(x) e Seno(x) com X tendendo a infinito
por lucasguilherme2 » Qui Mai 24, 2012 11:49
- 3 Respostas
- 44434 Exibições
- Última mensagem por LuizAquino

Ter Mai 29, 2012 11:54
Cálculo: Limites, Derivadas e Integrais
-
- Cosseno
por karen » Ter Nov 27, 2012 13:17
- 1 Respostas
- 1562 Exibições
- Última mensagem por MarceloFantini

Ter Nov 27, 2012 19:24
Trigonometria
-
- Cosseno (FUVEST)
 por Ananda » Sex Mar 14, 2008 22:37
por Ananda » Sex Mar 14, 2008 22:37
- 4 Respostas
- 6401 Exibições
- Última mensagem por Ananda

Seg Mar 17, 2008 17:28
Geometria Espacial
-
- Função Cosseno
por DanielFerreira » Qui Jul 30, 2009 17:41
- 1 Respostas
- 2869 Exibições
- Última mensagem por Felipe Schucman

Qui Jul 30, 2009 18:01
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





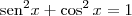 . Esclareça, por favor:
. Esclareça, por favor: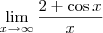 ou
ou 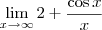 ?
?



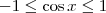
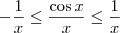
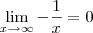 e
e 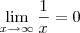 . Portanto, pelo Teorema do Sanduíche, segue que
. Portanto, pelo Teorema do Sanduíche, segue que 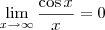 .
.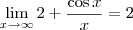 .
.






