 por LuizCarlos » Dom Ago 07, 2011 21:45
por LuizCarlos » Dom Ago 07, 2011 21:45
Ola, estou estudando, e não entendi um exemplo.
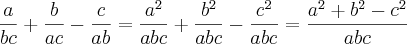
Não estou entendo por que abc foi reduzido ao mesmo denominador
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Neperiano » Dom Ago 07, 2011 22:00
por Neperiano » Dom Ago 07, 2011 22:00
Ola
Lembre se do mmc.
5/6 + 1/6 = 6/6 = 1
Quando o denominador é igual você só copia
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LuizCarlos » Dom Ago 07, 2011 22:13
por LuizCarlos » Dom Ago 07, 2011 22:13
Neperiano escreveu:Ola
Lembre se do mmc.
5/6 + 1/6 = 6/6 = 1
Quando o denominador é igual você só copia
Atenciosamente
blz, Neperiano, com números é tou entendo, mas tipo, com letras quero saber como que o denominador virou
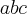
, quero saber como, o processo para se concluir que o denominador é
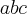
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Neperiano » Dom Ago 07, 2011 22:23
por Neperiano » Dom Ago 07, 2011 22:23
Ola
Faça mmc
a/bc + b/ac - c/ab
a^2 + b^2 - c^2
abc__abc__abc
Logo pelas propriedades você pode fizer que abc é o denominador de todos, e a outra forma de escreve é
(a^2 + b^2 - c^2)/abc
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LuizCarlos » Dom Ago 07, 2011 22:30
por LuizCarlos » Dom Ago 07, 2011 22:30
Neperiano escreveu:Ola
Faça mmc
a/bc + b/ac - c/ab
a^2 + b^2 - c^2
abc__abc__abc
Logo pelas propriedades você pode fizer que abc é o denominador de todos, e a outra forma de escreve é
(a^2 + b^2 - c^2)/abc
Atenciosamente
Ola Neperiano, faz esse mmc com letras ae pra eu ver, pois nao estou conseguindo fazer, nao estou entendo, como fazer mmc com letras.
Desde ja agradesço pela ajuda.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- frações algebricas
por tamirosa » Qui Out 29, 2009 20:11
- 1 Respostas
- 3307 Exibições
- Última mensagem por Molina

Sex Out 30, 2009 11:37
Álgebra Elementar
-
- Frações Algébricas
por LuizCarlos » Qui Abr 19, 2012 14:33
- 4 Respostas
- 2190 Exibições
- Última mensagem por LuizCarlos

Qui Abr 19, 2012 17:59
Álgebra Elementar
-
- Frações Algébricas Ajudem-me!
por Jansen » Seg Ago 31, 2009 23:32
- 0 Respostas
- 1673 Exibições
- Última mensagem por Jansen

Seg Ago 31, 2009 23:32
Sistemas de Equações
-
- Ajuda! Frações algébricas!
por vinik1 » Ter Mar 08, 2011 20:08
- 16 Respostas
- 9207 Exibições
- Última mensagem por MarceloFantini

Sáb Mar 12, 2011 18:17
Álgebra Elementar
-
- Dúvida em frações algébricas
por LuizCarlos » Dom Abr 22, 2012 10:04
- 7 Respostas
- 3230 Exibições
- Última mensagem por DanielFerreira

Qui Abr 26, 2012 20:14
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
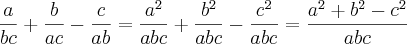

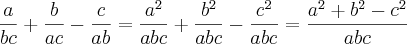


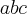 , quero saber como, o processo para se concluir que o denominador é
, quero saber como, o processo para se concluir que o denominador é 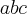



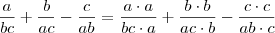
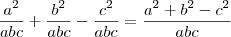


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.