 por LuizCarlos » Ter Ago 02, 2011 16:12
por LuizCarlos » Ter Ago 02, 2011 16:12
Produto Notaveis
Mensagempor Genilsonn » Ter 02 Ago, 2011 15:01
Resolvi esse produto notavel:
![(3a + \sqrt[]{3})^2 = 3a^2 + 2.3a.\sqrt[]{3} + (\sqrt[]{3})^2 = 9a^2 + 6a.\sqrt[]{3} + 3 (3a + \sqrt[]{3})^2 = 3a^2 + 2.3a.\sqrt[]{3} + (\sqrt[]{3})^2 = 9a^2 + 6a.\sqrt[]{3} + 3](/latexrender/pictures/47d6f788233e3cbcc8cd30f28627f897.png)
Só que no livro observei que a respota é :
![(3a + \sqrt[]{3})^2 = 3a^2 + 2.3a.\sqrt[]{3} + (\sqrt[]{3})^2 = 9a^2 + 6.\sqrt[]{3a} + 3 (3a + \sqrt[]{3})^2 = 3a^2 + 2.3a.\sqrt[]{3} + (\sqrt[]{3})^2 = 9a^2 + 6.\sqrt[]{3a} + 3](/latexrender/pictures/e422ccad8854031aaf8fa09cabc6bcd3.png)
Porque o radicando ficou com valor
![6.\sqrt[]{3a} 6.\sqrt[]{3a}](/latexrender/pictures/37c04cedaf649fea73ce5f4c475b01cb.png)
Não entendi.
Alguem me explique fazendo o favor? agradesço.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por MarceloFantini » Ter Ago 02, 2011 17:49
por MarceloFantini » Ter Ago 02, 2011 17:49
Acredito que o gabarito esteja errado, sua resolução está correta. Porém, não se esqueça dos parênteses:

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Qua Ago 03, 2011 02:13
por Claudin » Qua Ago 03, 2011 02:13
Caso tenha dificuldade em como, explorar este recurso de produtos notáveis, vou lhe apresentar alguns:
Neste link.

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizCarlos » Qua Ago 03, 2011 15:40
por LuizCarlos » Qua Ago 03, 2011 15:40
MarceloFantini escreveu:Acredito que o gabarito esteja errado, sua resolução está correta. Porém, não se esqueça dos parênteses:

.
Deixa eu ver si eu entendi, voce diz que
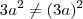
porque si fosse
![- 3a^2 = - 3a. 3a = - 9a^2 ? e se fosse [tex] (- 3a)^2 = (- 3a).(-3a) = 9a^2 - 3a^2 = - 3a. 3a = - 9a^2 ? e se fosse [tex] (- 3a)^2 = (- 3a).(-3a) = 9a^2](/latexrender/pictures/94971682b2dc5067c4bfa186ae50682a.png)
é isso ?
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Claudin » Qua Ago 03, 2011 15:52
por Claudin » Qua Ago 03, 2011 15:52
LuizCarlos escreveu:Deixa eu ver si eu entendi, voce diz que
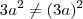
porque si fosse
![- 3a^2 = - 3a. 3a = - 9a^2 ? e se fosse [tex] (- 3a)^2 = (- 3a).(-3a) = 9a^2 - 3a^2 = - 3a. 3a = - 9a^2 ? e se fosse [tex] (- 3a)^2 = (- 3a).(-3a) = 9a^2](/latexrender/pictures/94971682b2dc5067c4bfa186ae50682a.png)
é isso ?
Seria o seguinte:
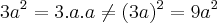
Vendo outro caso:
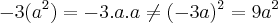
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizCarlos » Qui Ago 04, 2011 00:57
por LuizCarlos » Qui Ago 04, 2011 00:57
Claudin escreveu:LuizCarlos escreveu:Deixa eu ver si eu entendi, voce diz que
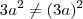
porque si fosse
![- 3a^2 = - 3a. 3a = - 9a^2 ? e se fosse [tex] (- 3a)^2 = (- 3a).(-3a) = 9a^2 - 3a^2 = - 3a. 3a = - 9a^2 ? e se fosse [tex] (- 3a)^2 = (- 3a).(-3a) = 9a^2](/latexrender/pictures/94971682b2dc5067c4bfa186ae50682a.png)
é isso ?
Seria o seguinte:
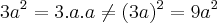
Vendo outro caso:
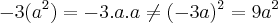
Entendi agora Claudin, perfeito, muito obrigado.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Claudin » Qui Ago 04, 2011 03:00
por Claudin » Qui Ago 04, 2011 03:00
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Produto Notáveis
por Flavio Cacequi » Sex Mar 30, 2018 20:55
- 1 Respostas
- 3545 Exibições
- Última mensagem por Gebe

Sáb Mar 31, 2018 13:21
Álgebra Elementar
-
- Produto escalar, Produto Vetorial e Produto Misto
 por fernando7 » Qua Mai 23, 2018 17:29
por fernando7 » Qua Mai 23, 2018 17:29
- 0 Respostas
- 4944 Exibições
- Última mensagem por fernando7

Qua Mai 23, 2018 17:29
Geometria Analítica
-
- Limites Notáveis
por spoof » Qui Out 14, 2010 11:23
- 2 Respostas
- 5246 Exibições
- Última mensagem por spoof

Sex Out 15, 2010 14:20
Cálculo: Limites, Derivadas e Integrais
-
- Produtos Notáveis
por Du21 » Ter Mar 29, 2011 20:31
- 2 Respostas
- 2338 Exibições
- Última mensagem por Du21

Ter Mar 29, 2011 21:02
Álgebra Elementar
-
- Quadriláteros notáveis
 por Jean Cigari » Qua Jun 22, 2011 11:26
por Jean Cigari » Qua Jun 22, 2011 11:26
- 2 Respostas
- 14910 Exibições
- Última mensagem por Jean Cigari

Qua Jun 22, 2011 22:30
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![(3a + \sqrt[]{3})^2 = 3a^2 + 2.3a.\sqrt[]{3} + (\sqrt[]{3})^2 = 9a^2 + 6a.\sqrt[]{3} + 3 (3a + \sqrt[]{3})^2 = 3a^2 + 2.3a.\sqrt[]{3} + (\sqrt[]{3})^2 = 9a^2 + 6a.\sqrt[]{3} + 3](/latexrender/pictures/47d6f788233e3cbcc8cd30f28627f897.png)
![(3a + \sqrt[]{3})^2 = 3a^2 + 2.3a.\sqrt[]{3} + (\sqrt[]{3})^2 = 9a^2 + 6.\sqrt[]{3a} + 3 (3a + \sqrt[]{3})^2 = 3a^2 + 2.3a.\sqrt[]{3} + (\sqrt[]{3})^2 = 9a^2 + 6.\sqrt[]{3a} + 3](/latexrender/pictures/e422ccad8854031aaf8fa09cabc6bcd3.png)
![6.\sqrt[]{3a} 6.\sqrt[]{3a}](/latexrender/pictures/37c04cedaf649fea73ce5f4c475b01cb.png)

![(3a + \sqrt[]{3})^2 = 3a^2 + 2.3a.\sqrt[]{3} + (\sqrt[]{3})^2 = 9a^2 + 6a.\sqrt[]{3} + 3 (3a + \sqrt[]{3})^2 = 3a^2 + 2.3a.\sqrt[]{3} + (\sqrt[]{3})^2 = 9a^2 + 6a.\sqrt[]{3} + 3](/latexrender/pictures/47d6f788233e3cbcc8cd30f28627f897.png)
![(3a + \sqrt[]{3})^2 = 3a^2 + 2.3a.\sqrt[]{3} + (\sqrt[]{3})^2 = 9a^2 + 6.\sqrt[]{3a} + 3 (3a + \sqrt[]{3})^2 = 3a^2 + 2.3a.\sqrt[]{3} + (\sqrt[]{3})^2 = 9a^2 + 6.\sqrt[]{3a} + 3](/latexrender/pictures/e422ccad8854031aaf8fa09cabc6bcd3.png)
![6.\sqrt[]{3a} 6.\sqrt[]{3a}](/latexrender/pictures/37c04cedaf649fea73ce5f4c475b01cb.png)

 .
.



.
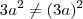 porque si fosse
porque si fosse ![- 3a^2 = - 3a. 3a = - 9a^2 ? e se fosse [tex] (- 3a)^2 = (- 3a).(-3a) = 9a^2 - 3a^2 = - 3a. 3a = - 9a^2 ? e se fosse [tex] (- 3a)^2 = (- 3a).(-3a) = 9a^2](/latexrender/pictures/94971682b2dc5067c4bfa186ae50682a.png) é isso ?
é isso ?
porque si fosse
é isso ?
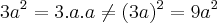
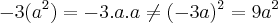

porque si fosse
é isso ?


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
