 por alexandreredefor » Sex Jul 15, 2011 16:51
por alexandreredefor » Sex Jul 15, 2011 16:51
sejam f e g funções tais que

, onde k é uma constante e
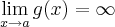
. Prove que

Editado pela última vez por
alexandreredefor em Sex Jul 15, 2011 21:10, em um total de 1 vez.
-
alexandreredefor
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Jul 15, 2011 10:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por LuizAquino » Sex Jul 15, 2011 17:05
por LuizAquino » Sex Jul 15, 2011 17:05
O que você já tentou fazer? Onde está exatamente a sua dúvida?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por alexandreredefor » Sex Jul 15, 2011 17:18
por alexandreredefor » Sex Jul 15, 2011 17:18
não sei por onde começar sera que posso usar a propriedade
-
alexandreredefor
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Jul 15, 2011 10:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por LuizAquino » Sex Jul 15, 2011 17:52
por LuizAquino » Sex Jul 15, 2011 17:52
Se já tiver sido provado as propriedades operatórios dos limites, então basta utilizá-las.
Caso contrário, você terá que provar usando a definição de limites.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por LuizAquino » Sex Jul 15, 2011 21:29
por LuizAquino » Sex Jul 15, 2011 21:29
Vejamos como fazer utilizando as definições de limites.
Eu vou considerar que o símbolo

significa

.
Temos duas hipótese:
(i)
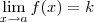
Por definição: para todo

, existe

tal que
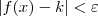
sempre que

.
(ii)

Por definição: para todo

, existe

tal que
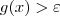
sempre que

.
A tese será:
(iii)
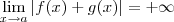
Por definição: para todo

, existe

tal que

sempre que

.
DemonstraçãoSeja

. Considere o número

.
Se

, então pela hipótese (ii) existe

tal que
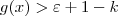
sempre que

.
Se

, então pela hipótese (ii) existe

tal que
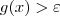
sempre que

. Mas como

, temos que
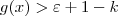
.
Por outro lado, sabemos que 1 é um número positivo. Portanto, pela hipótese (i) existe

tal que
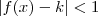
sempre que

. Mas de
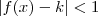
, nós obtemos que

. Ou seja, temos que

.
Tome
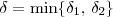
. Pelo que foi exposto acima, temos que para esse número

as duas inequações abaixo vão ocorrer sempre que

:
(1)
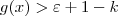
(2)

Somando (1) e (2), obtemos
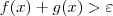
.
Pela hipótese (ii), nas proximidade de
a a função
g é tal que
g > 0.
Além disso, perceba que das duas hipóteses podemos concluir que nas proximidade de
a as funções
f e
g são tais que
g >>
f (isto é,
g é muito maior do que
f).
Desse modo, teremos que nas proximidades de
a irá ocorrer |
f +
g| =
f +
g.
Logo, obtemos que

.
#
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Sex Jul 15, 2011 22:04
por MarceloFantini » Sex Jul 15, 2011 22:04
Luiz, seria interessante mostrar porque da escolha de

, para que não pareça que "caiu do céu".
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sex Jul 15, 2011 22:12
por LuizAquino » Sex Jul 15, 2011 22:12
MarceloFantini escreveu:Luiz, seria interessante mostrar porque da escolha de

, para que não pareça que "caiu do céu".
O artifício de tomar esse número leva em consideração o pensamento de que no final precisamos realizar uma soma entre inequações do tipo

e
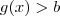
de modo a obter
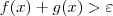
. Sendo assim, precisamos construir uma estratégia de modo que
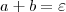
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Prova - dúvida
por marinalcd » Sex Fev 21, 2014 20:48
- 1 Respostas
- 915 Exibições
- Última mensagem por DanielFerreira

Sex Fev 21, 2014 22:15
Cálculo: Limites, Derivadas e Integrais
-
- duvida de uma prova AJUDEM
por lais_banestes » Qua Mai 16, 2012 21:45
- 0 Respostas
- 1160 Exibições
- Última mensagem por lais_banestes

Qua Mai 16, 2012 21:45
Estatística
-
- Questão prova concurso (dúvida)
por fernandocez » Seg Mar 14, 2011 21:35
- 5 Respostas
- 2676 Exibições
- Última mensagem por fernandocez

Qua Mar 16, 2011 00:16
Logaritmos
-
- Dúvida de P.A (Exercício prova SENAI)
por Bia_Oliveira » Qua Set 26, 2012 09:53
- 2 Respostas
- 2339 Exibições
- Última mensagem por Bia_Oliveira

Dom Set 30, 2012 11:45
Progressões
-
- Questão prova concurso (dúvida na resposta)
 por fernandocez » Qua Mar 16, 2011 13:47
por fernandocez » Qua Mar 16, 2011 13:47
- 3 Respostas
- 2953 Exibições
- Última mensagem por fernandocez

Qua Mar 16, 2011 23:36
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , onde k é uma constante e
, onde k é uma constante e 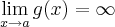 . Prove que
. Prove que 

 , onde k é uma constante e
, onde k é uma constante e 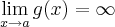 . Prove que
. Prove que 




 significa
significa  .
.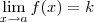
 , existe
, existe  tal que
tal que 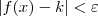 sempre que
sempre que  .
.
 , existe
, existe  tal que
tal que 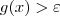 sempre que
sempre que  .
.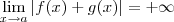
 , existe
, existe  tal que
tal que  sempre que
sempre que  .
. . Considere o número
. Considere o número  .
. , então pela hipótese (ii) existe
, então pela hipótese (ii) existe  tal que
tal que 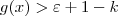 sempre que
sempre que  .
. , então pela hipótese (ii) existe
, então pela hipótese (ii) existe  tal que
tal que 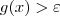 sempre que
sempre que  . Mas como
. Mas como  , temos que
, temos que 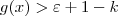 .
. tal que
tal que 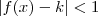 sempre que
sempre que  . Mas de
. Mas de 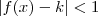 , nós obtemos que
, nós obtemos que  . Ou seja, temos que
. Ou seja, temos que  .
.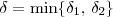 . Pelo que foi exposto acima, temos que para esse número
. Pelo que foi exposto acima, temos que para esse número  as duas inequações abaixo vão ocorrer sempre que
as duas inequações abaixo vão ocorrer sempre que  :
: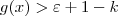

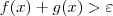 .
. .
.
 , para que não pareça que "caiu do céu".
, para que não pareça que "caiu do céu".

, para que não pareça que "caiu do céu".
 e
e 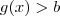 de modo a obter
de modo a obter 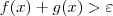 . Sendo assim, precisamos construir uma estratégia de modo que
. Sendo assim, precisamos construir uma estratégia de modo que 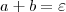 .
.


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.