 , onde k é uma constante e
, onde k é uma constante e 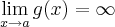 . Prove que
. Prove que 

 , onde k é uma constante e
, onde k é uma constante e 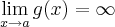 . Prove que
. Prove que 




 significa
significa  .
.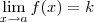
 , existe
, existe  tal que
tal que 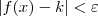 sempre que
sempre que  .
.
 , existe
, existe  tal que
tal que 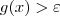 sempre que
sempre que  .
.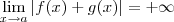
 , existe
, existe  tal que
tal que  sempre que
sempre que  .
. . Considere o número
. Considere o número  .
. , então pela hipótese (ii) existe
, então pela hipótese (ii) existe  tal que
tal que 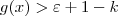 sempre que
sempre que  .
. , então pela hipótese (ii) existe
, então pela hipótese (ii) existe  tal que
tal que 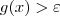 sempre que
sempre que  . Mas como
. Mas como  , temos que
, temos que 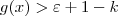 .
. tal que
tal que 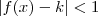 sempre que
sempre que  . Mas de
. Mas de 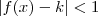 , nós obtemos que
, nós obtemos que  . Ou seja, temos que
. Ou seja, temos que  .
.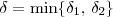 . Pelo que foi exposto acima, temos que para esse número
. Pelo que foi exposto acima, temos que para esse número  as duas inequações abaixo vão ocorrer sempre que
as duas inequações abaixo vão ocorrer sempre que  :
: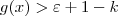

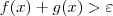 .
. .
.
 , para que não pareça que "caiu do céu".
, para que não pareça que "caiu do céu".

MarceloFantini escreveu:Luiz, seria interessante mostrar porque da escolha de, para que não pareça que "caiu do céu".
 e
e 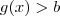 de modo a obter
de modo a obter 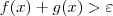 . Sendo assim, precisamos construir uma estratégia de modo que
. Sendo assim, precisamos construir uma estratégia de modo que 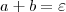 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

