Gente, eu to com uma dúvida aqui a respeito de uma inequação que envolve soma de módulos. A inequação é:
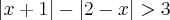 .
.Eu não estou conseguindo fazer essa soma. Tentei aplicar as propriedae de módulo, mas o x anulou... Tenho um monte de questões assim pra resolver, mas tô meio perdida. Eu sempre coloco aqui o modo como eu tentei resolver, mas é que dessa vez eu não tô nem sabendo começar...

Tem um outro tipo de inequação modular aqui que eu também não tô sabendo fazer... Acho que meu problema é com o módulo!!

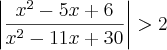
Se alguém puder me ajudar agredeço muitíssimo!!
Se puder colocar a resolução completa pra eu poder acompanhar também agradeço muito!!!

Beijos!!



 é zero quando
é zero quando 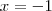 , positivo quando
, positivo quando  e negativo quando
e negativo quando 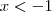
 é zero quando
é zero quando  , positivo quando
, positivo quando 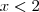 e negativo quando
e negativo quando 

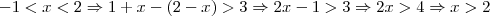
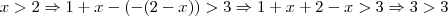


 para depois verificar caso a caso e retirar o módulo.
para depois verificar caso a caso e retirar o módulo.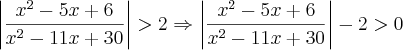
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.