![\lim_{x\rightarrow0} \frac{\sqrt[]{x+2}-\sqrt[]{2}}{x} \lim_{x\rightarrow0} \frac{\sqrt[]{x+2}-\sqrt[]{2}}{x}](/latexrender/pictures/9a16ce063de2c4eef6dcb94f73764598.png)
Gostaria de saber qual o valor correto da resolução. Seria
 ?
?
![\lim_{x\rightarrow0} \frac{\sqrt[]{x+2}-\sqrt[]{2}}{x} \lim_{x\rightarrow0} \frac{\sqrt[]{x+2}-\sqrt[]{2}}{x}](/latexrender/pictures/9a16ce063de2c4eef6dcb94f73764598.png)
 ?
?

stuart clark escreveu:
![\lim_{x\rightarrow0}\frac{\sqrt[]{x+2}-\sqrt[]{2}}{x} \Rightarrow \lim_{x\rightarrow0}\frac{\sqrt[]{x+2}-\sqrt[]{2}}{x}. \frac{\sqrt[]{x+2}+\sqrt[]{2}}{\sqrt[]{x+2}+\sqrt[]{2}} \lim_{x\rightarrow0}\frac{\sqrt[]{x+2}-\sqrt[]{2}}{x} \Rightarrow \lim_{x\rightarrow0}\frac{\sqrt[]{x+2}-\sqrt[]{2}}{x}. \frac{\sqrt[]{x+2}+\sqrt[]{2}}{\sqrt[]{x+2}+\sqrt[]{2}}](/latexrender/pictures/e6c68bec1e8719ee80f42282da79ecb8.png)
![\Rightarrow\lim_{x\rightarrow0}\frac{x+2-2}{x(\sqrt[]{x+2}+\sqrt[]{2})}\Rightarrow\lim_{x\rightarrow0}\frac{x}{x(\sqrt[]{x+2}+\sqrt[]{2})}\Rightarrow\lim_{x\rightarrow0}\frac{(1)^2}{(\sqrt[]{x+2})^2+(\sqrt[]{2})^2} \Rightarrow\lim_{x\rightarrow0}\frac{x+2-2}{x(\sqrt[]{x+2}+\sqrt[]{2})}\Rightarrow\lim_{x\rightarrow0}\frac{x}{x(\sqrt[]{x+2}+\sqrt[]{2})}\Rightarrow\lim_{x\rightarrow0}\frac{(1)^2}{(\sqrt[]{x+2})^2+(\sqrt[]{2})^2}](/latexrender/pictures/6a58e35d8b816dfd596f8e22416bb577.png)
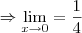


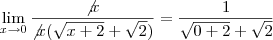
 o que é igual a
o que é igual a 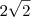 não 4... rs ok?
não 4... rs ok?

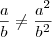 , certo?
, certo?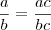 , não é verdade?
, não é verdade?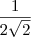 ainda não é o resultado final, segundo creio, pois uma raíz no denominador é inadequada... então, seria melhor continuar, multiplicando ambos pela raiz, chegando a
ainda não é o resultado final, segundo creio, pois uma raíz no denominador é inadequada... então, seria melhor continuar, multiplicando ambos pela raiz, chegando a 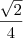


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)