 por Claudin » Ter Mai 31, 2011 12:17
por Claudin » Ter Mai 31, 2011 12:17
![\lim_{x\rightarrow0} \frac{\sqrt[]{x+2}-\sqrt[]{2}}{x} \lim_{x\rightarrow0} \frac{\sqrt[]{x+2}-\sqrt[]{2}}{x}](/latexrender/pictures/9a16ce063de2c4eef6dcb94f73764598.png)
Gostaria de saber qual o valor correto da resolução. Seria

?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por stuart clark » Ter Mai 31, 2011 13:59
por stuart clark » Ter Mai 31, 2011 13:59
-
stuart clark
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Mai 28, 2011 00:32
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Claudin » Ter Mai 31, 2011 15:21
por Claudin » Ter Mai 31, 2011 15:21
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por carlosalesouza » Ter Mai 31, 2011 17:27
por carlosalesouza » Ter Mai 31, 2011 17:27
Claudin, creio que vc ta cometendo uma pequena distração... rs
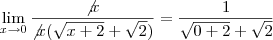
Agora, no denominador, temos

o que é igual a
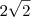
não 4... rs ok?
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por Claudin » Ter Mai 31, 2011 17:30
por Claudin » Ter Mai 31, 2011 17:30
Elevei tanto o numerador como denominador ao quadrado para retirar a raiz.
E depois de tirar a raiz, que substitui "x" tendendo a zero. que ficaria 0+2+2
Entendeu oq eu fiz? Só queria saber se isso pode ser feito
Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por carlosalesouza » Ter Mai 31, 2011 17:49
por carlosalesouza » Ter Mai 31, 2011 17:49
Elevar ao quadrado só pode ser feito quando temos uma (des)igualdade... pois,
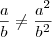
, certo?
Quando temos apenas uma fração, o que podemos fazer é multiplicar ou dividir numerador e denominar por um mesmo valor, pois
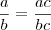
, não é verdade?
Por isso que acabou dando um resultado diferente...
é verdade que
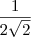
ainda não é o resultado final, segundo creio, pois uma raíz no denominador é inadequada... então, seria melhor continuar, multiplicando ambos pela raiz, chegando a
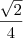
Que me pareceria uma resposta mais elegante... hehehehe
Uma abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por Claudin » Ter Mai 31, 2011 17:51
por Claudin » Ter Mai 31, 2011 17:51
Concordo, Valeu pela ajuda Carlos
Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6642 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4789 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5118 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7257 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4434 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow0} \frac{\sqrt[]{x+2}-\sqrt[]{2}}{x} \lim_{x\rightarrow0} \frac{\sqrt[]{x+2}-\sqrt[]{2}}{x}](/latexrender/pictures/9a16ce063de2c4eef6dcb94f73764598.png)
 ?
?
![\lim_{x\rightarrow0} \frac{\sqrt[]{x+2}-\sqrt[]{2}}{x} \lim_{x\rightarrow0} \frac{\sqrt[]{x+2}-\sqrt[]{2}}{x}](/latexrender/pictures/9a16ce063de2c4eef6dcb94f73764598.png)
 ?
?

![\lim_{x\rightarrow0}\frac{\sqrt[]{x+2}-\sqrt[]{2}}{x} \Rightarrow \lim_{x\rightarrow0}\frac{\sqrt[]{x+2}-\sqrt[]{2}}{x}. \frac{\sqrt[]{x+2}+\sqrt[]{2}}{\sqrt[]{x+2}+\sqrt[]{2}} \lim_{x\rightarrow0}\frac{\sqrt[]{x+2}-\sqrt[]{2}}{x} \Rightarrow \lim_{x\rightarrow0}\frac{\sqrt[]{x+2}-\sqrt[]{2}}{x}. \frac{\sqrt[]{x+2}+\sqrt[]{2}}{\sqrt[]{x+2}+\sqrt[]{2}}](/latexrender/pictures/e6c68bec1e8719ee80f42282da79ecb8.png)
![\Rightarrow\lim_{x\rightarrow0}\frac{x+2-2}{x(\sqrt[]{x+2}+\sqrt[]{2})}\Rightarrow\lim_{x\rightarrow0}\frac{x}{x(\sqrt[]{x+2}+\sqrt[]{2})}\Rightarrow\lim_{x\rightarrow0}\frac{(1)^2}{(\sqrt[]{x+2})^2+(\sqrt[]{2})^2} \Rightarrow\lim_{x\rightarrow0}\frac{x+2-2}{x(\sqrt[]{x+2}+\sqrt[]{2})}\Rightarrow\lim_{x\rightarrow0}\frac{x}{x(\sqrt[]{x+2}+\sqrt[]{2})}\Rightarrow\lim_{x\rightarrow0}\frac{(1)^2}{(\sqrt[]{x+2})^2+(\sqrt[]{2})^2}](/latexrender/pictures/6a58e35d8b816dfd596f8e22416bb577.png)
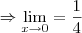


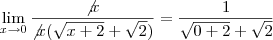
 o que é igual a
o que é igual a 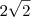 não 4... rs ok?
não 4... rs ok?

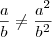 , certo?
, certo?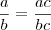 , não é verdade?
, não é verdade?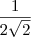 ainda não é o resultado final, segundo creio, pois uma raíz no denominador é inadequada... então, seria melhor continuar, multiplicando ambos pela raiz, chegando a
ainda não é o resultado final, segundo creio, pois uma raíz no denominador é inadequada... então, seria melhor continuar, multiplicando ambos pela raiz, chegando a 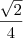


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
