![\lim_{x\rightarrow+\infty}\frac{\frac{1}{x^6}+(x^{-4})^2-(14x^3)^{-5}}{\frac{(x^{20})^{-1}}{(\sqrt[6]{x^{20})}^{-1}}+\sqrt[5]{4x^6}}](/latexrender/pictures/7383706c8dc7363144435e556cca93ca.png "\lim_{x\rightarrow+\infty}\frac{\frac{1}{x^6}+(x^{-4})^2-(14x^3)^{-5}}{\frac{(x^{20})^{-1}}{(\sqrt[6]{x^{20})}^{-1}}+\sqrt[5]{4x^6}}")
Nao consegui concluir o exercicio
algm para ajudar?
obrigado
por Claudin » Seg Mai 23, 2011 18:43
por Claudin » Seg Mai 23, 2011 18:49
por LuizAquino » Seg Mai 23, 2011 23:22
![\lim_{x\to +\infty}\frac{\frac{1}{x^6}+(x^{-4})^2-(14x^3)^{-5}}{\frac{(x^{20})^{-1}}{(\sqrt[6]{x^{20}})^{-1}}+\sqrt[5]{4x^6}}](/latexrender/pictures/cfeb68536e8b581f9e864d80553d9064.png "\lim_{x\to +\infty}\frac{\frac{1}{x^6}+(x^{-4})^2-(14x^3)^{-5}}{\frac{(x^{20})^{-1}}{(\sqrt[6]{x^{20}})^{-1}}+\sqrt[5]{4x^6}}")
![\,= \lim_{x\to +\infty}\frac{\frac{1}{x^6}+\frac{1}{x^8}-\frac{1}{14^5x^{15}}}{\frac{\sqrt[6]{x^{20}}}{x^{20}}+\sqrt[5]{4x^6}}](/latexrender/pictures/9de2bfefc652dca3ed98d6bb1123b2f9.png "\,= \lim_{x\to +\infty}\frac{\frac{1}{x^6}+\frac{1}{x^8}-\frac{1}{14^5x^{15}}}{\frac{\sqrt[6]{x^{20}}}{x^{20}}+\sqrt[5]{4x^6}}")
![= \lim_{x\to +\infty}\frac{\frac{1}{x^6\sqrt[5]{4x^6}}+\frac{1}{x^8\sqrt[5]{4x^6}}-\frac{1}{14^5x^{15}\sqrt[5]{4x^6}}}{\frac{1}{\sqrt[5]{4x^6}}\sqrt[6]{\frac{1}{x^{100}}}+1}](/latexrender/pictures/e3f266ebc49a220bcf63c4c5dd23ca0c.png "= \lim_{x\to +\infty}\frac{\frac{1}{x^6\sqrt[5]{4x^6}}+\frac{1}{x^8\sqrt[5]{4x^6}}-\frac{1}{14^5x^{15}\sqrt[5]{4x^6}}}{\frac{1}{\sqrt[5]{4x^6}}\sqrt[6]{\frac{1}{x^{100}}}+1}")
por Claudin » Qua Mai 25, 2011 17:49
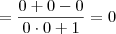
![(\frac{x^{20}}{\sqrt[6]{x^{20}}})^{-1}](/latexrender/pictures/f41782bdb5418f031ed4f6a0731055cd.png "(\frac{x^{20}}{\sqrt[6]{x^{20}}})^{-1}")
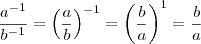por LuizAquino » Qua Mai 25, 2011 19:51
.![\frac{\sqrt[n]{a}}{b} = \sqrt[n]{\frac{a}{b^n}}](/latexrender/pictures/008eb28d9eff1c44eb73c413942a828c.png "\frac{\sqrt[n]{a}}{b} = \sqrt[n]{\frac{a}{b^n}}")
,por Claudin » Qua Mai 25, 2011 19:53
![\sqrt[6]{\frac{1}{x^{100}}}+1](/latexrender/pictures/ca82711f044690481f21c9435294b92a.png "\sqrt[6]{\frac{1}{x^{100}}}+1")
por LuizAquino » Qua Mai 25, 2011 20:27
![\sqrt[5]{4x^6}](/latexrender/pictures/165ff28f72d8c1ec592a8810e2fc198c.png "\sqrt[5]{4x^6}")
.por Claudin » Qui Mai 26, 2011 11:31
![\sqrt[6]{\frac{x^{20}}{(x^{20})^{6}}} . \frac{1}{\sqrt[5]{4x^6}} + 1](/latexrender/pictures/9caf56e5af9bddadc0e5c22549089be5.png "\sqrt[6]{\frac{x^{20}}{(x^{20})^{6}}} . \frac{1}{\sqrt[5]{4x^6}} + 1")
por Claudin » Qui Mai 26, 2011 22:33
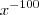e não retirei a potência por isso nao estava encontrando o resultado!Voltar para Cálculo: Limites, Derivadas e Integrais
por Raphaela_sf » Qui Abr 05, 2012 19:26
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)![\sqrt[6]{\frac{x^{20}}{(x^{20})^{6}}}=\sqrt[6]{\frac{x^{20}}{x^{20.6}}}=\sqrt[6]{\frac{x^{20}}{x^{120}}}=\sqrt[6]{\frac{1}{x^{120-20}}}=\sqrt[6]{\frac{1}{x^{100}}}](/latexrender/pictures/9019b2dae85bad74dc0f03dbd68a3d7d.png "\sqrt[6]{\frac{x^{20}}{(x^{20})^{6}}}=\sqrt[6]{\frac{x^{20}}{x^{20.6}}}=\sqrt[6]{\frac{x^{20}}{x^{120}}}=\sqrt[6]{\frac{1}{x^{120-20}}}=\sqrt[6]{\frac{1}{x^{100}}}")