 por jamiel » Sáb Mai 14, 2011 15:40
por jamiel » Sáb Mai 14, 2011 15:40
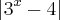
Eu fiz x=4/3, mas vejo q não zera a função. A reta esquerda do gráfico q corta a ordenada y é igual |-1|=1. Estou muito confuso quanto a resolução dessa função.
Não sei ao certo se "3^(4/3)" daria o prório "3" ou "4, ... alguma coisa". Alguém pode dar uma dica?
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Sáb Mai 14, 2011 17:29
por MarceloFantini » Sáb Mai 14, 2011 17:29
O valor onde zera a função é

.Para x antes disso, ela é negativa e portanto

, e para depois disso positiva e portanto

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jamiel » Dom Mai 15, 2011 09:41
por jamiel » Dom Mai 15, 2011 09:41

Putz! Como não pude perceber isso? Seria esse o raciocínio?
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Dom Mai 15, 2011 09:49
por MarceloFantini » Dom Mai 15, 2011 09:49
Não, não é isso, e pior ainda: está errando conceitos fundamentais.

, e não

. Para verificar, basta colocar numa calculadora (eles são próximos, mas não iguais).
O raciocínio é que existe um a real
fixo tal que a função zere, ou seja,

. Para valores de x maiores que este, o módulo da diferença é maior que zero, portanto permanece igual. Para valores de x menores que este, o módulo da diferença é menor que zero, portanto multiplicamos o que está dentro por -1 e retiramos o módulo. Então, a curva para
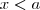
é

, 0 quando

e

quando
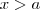
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jamiel » Dom Mai 15, 2011 10:12
por jamiel » Dom Mai 15, 2011 10:12
rsrs fiquei confuso com essa. Vejamos, a função zero quando x=1,3, certo? 3*1,3=4!
Se a função modular fosse |3x-4| o gráfico teria origem x em 4/3(1,3) e cortaria y em 4 . Nesse caso q apresentei "3^1,3 -4" o resultado desse diferença seria "0". O q eu quero dizer, na verdade, é q em |3x-4| o gráfico tem origem em x=4/3 e a parte inclinada corta a ordenada em y=4. Já em |3^x-4), a reta corta y em 3. Não estou assimilando essa parte, eu sei q se eu pôr valores arbitrarios eu chego em 3, mas não estou vendo isso de prima, entende?
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Dom Mai 15, 2011 10:22
por MarceloFantini » Dom Mai 15, 2011 10:22
Jamiel,
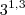 NÃO É
NÃO É 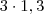
. Pense: o que significa uma função "cortar" o eixo y? Significa que

. Se você fizer x=0, temos que
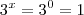
, e leva a

. Note também que as funções

e

são MUITO diferentes. Primeiro,

nunca zera (perceba que falo APENAS de

e não

). Segundo,

nunca é negativa, e cresce mais rápido que

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jamiel » Dom Mai 15, 2011 10:40
por jamiel » Dom Mai 15, 2011 10:40
Ok. Então, o conceito nesse caso é diferente. Eu não posso simplesmente considerar o "-4" como parte do gráfico cortando o eixo y em "4"? Como há uma "exponencial" dentro do modulo, devo considerar x=0 para poder saber onde exatamente o o gráfico corta y?
Foi mau, tow meio enrolado! rsrs
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função exponencial] Problema
por fff » Sáb Abr 12, 2014 17:17
- 0 Respostas
- 1051 Exibições
- Última mensagem por fff

Sáb Abr 12, 2014 17:17
Logaritmos
-
- [Função exponencial e logaritmica] Problema
por fff » Sáb Jan 04, 2014 12:02
- 2 Respostas
- 1350 Exibições
- Última mensagem por fff

Seg Jan 06, 2014 12:19
Funções
-
- [Derivada de Função Exponencial] Problema de Economia
por Ronaldobb » Seg Out 29, 2012 09:38
- 1 Respostas
- 1502 Exibições
- Última mensagem por e8group

Seg Out 29, 2012 11:54
Cálculo: Limites, Derivadas e Integrais
-
- [Função exponencial] Exercício sobre função exponencial
por fff » Ter Jan 07, 2014 17:51
- 3 Respostas
- 4072 Exibições
- Última mensagem por fff

Qua Jan 08, 2014 06:47
Funções
-
- Problema Com Inequação do Exponencial
por chenz » Sáb Jun 19, 2010 17:13
- 2 Respostas
- 1767 Exibições
- Última mensagem por chenz

Dom Jun 20, 2010 12:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
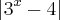


 .Para x antes disso, ela é negativa e portanto
.Para x antes disso, ela é negativa e portanto  , e para depois disso positiva e portanto
, e para depois disso positiva e portanto  .
.


 , e não
, e não  . Para verificar, basta colocar numa calculadora (eles são próximos, mas não iguais).
. Para verificar, basta colocar numa calculadora (eles são próximos, mas não iguais).  . Para valores de x maiores que este, o módulo da diferença é maior que zero, portanto permanece igual. Para valores de x menores que este, o módulo da diferença é menor que zero, portanto multiplicamos o que está dentro por -1 e retiramos o módulo. Então, a curva para
. Para valores de x maiores que este, o módulo da diferença é maior que zero, portanto permanece igual. Para valores de x menores que este, o módulo da diferença é menor que zero, portanto multiplicamos o que está dentro por -1 e retiramos o módulo. Então, a curva para 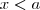 é
é  e
e 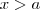 .
.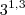
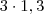 . Pense: o que significa uma função "cortar" o eixo y? Significa que
. Pense: o que significa uma função "cortar" o eixo y? Significa que  . Se você fizer x=0, temos que
. Se você fizer x=0, temos que 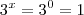 , e leva a
, e leva a  . Note também que as funções
. Note também que as funções  e
e  são MUITO diferentes. Primeiro,
são MUITO diferentes. Primeiro, ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.