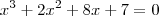 ,sabendo que o polinomio
,sabendo que o polinomio p(x)=
 é divisivel por x+1.
é divisivel por x+1.me ajudem ai tentei de todas as formas entender o enunciado mais nau consegui chegar a nenhuma resposta
me ajudem ai.
eu tentei usar a formula de B. ruffini mais da uma equaçao do 2° grau q nau tem soluçao!
qual formula devo usar ou onde estou errando!
obrigado






![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)