 por willwgo » Qui Abr 28, 2011 18:15
por willwgo » Qui Abr 28, 2011 18:15
Calcule os valores reais de x para que:
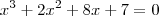
,sabendo que o polinomio
p(x)=

é divisivel por x+1.
me ajudem ai tentei de todas as formas entender o enunciado mais nau consegui chegar a nenhuma resposta
me ajudem ai.
eu tentei usar a formula de B. ruffini mais da uma equaçao do 2° grau q nau tem soluçao!
qual formula devo usar ou onde estou errando!
obrigado
-
willwgo
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qui Fev 17, 2011 15:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Qui Abr 28, 2011 18:56
por Molina » Qui Abr 28, 2011 18:56
Boa tarde.
Quando você diz que não tem solução a equação do 2o grau é nos números Reais, certo? Mas elas existem no conjunto dos complexos...

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por willwgo » Sex Abr 29, 2011 17:35
por willwgo » Sex Abr 29, 2011 17:35
é q o delta deu um valor negativo!
vc poderia me passar a resposta q vc axou p/ eu tentar chegar a tal resposta sozinho!
obrigado
-
willwgo
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qui Fev 17, 2011 15:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Renato_RJ » Sex Abr 29, 2011 21:11
por Renato_RJ » Sex Abr 29, 2011 21:11
Campeão, se o polinômio p(x) é divisível por (x+1) então teremos:

Digo isso, pois como foi dito no enunciado P(x) é divisível por (x+1), logo não há resto.
Como você mesmo disse, Q(x) será um polinômio de 2º grau com delta negativo, logo suas raízes não pertencem ao domínio dos Reais, mas lembre-se que P(x) é igual ao Q(x) * (x+1), então uma das raízes pertence a x+1, logo será -1 (que pertence aos Reais).
Acho que a resposta que você procura seja essa.
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Quais os possíveis valores que satisfazem os valores reais
por andersontricordiano » Seg Fev 24, 2014 22:53
- 1 Respostas
- 5153 Exibições
- Última mensagem por Russman

Ter Fev 25, 2014 02:17
Números Complexos
-
- Calcule qual quadrante pertence os numeros reais
por andersontricordiano » Ter Jun 07, 2011 20:19
- 1 Respostas
- 1677 Exibições
- Última mensagem por Capelett

Sex Jun 17, 2011 23:39
Trigonometria
-
- zeros reais de funções reais
por bebelo32 » Dom Mar 11, 2018 21:12
- 2 Respostas
- 5503 Exibições
- Última mensagem por adauto martins

Seg Abr 23, 2018 17:52
Funções
-
- Números Reais - Simplificar números reais
por ZANGARO » Ter Nov 15, 2011 18:46
- 0 Respostas
- 1943 Exibições
- Última mensagem por ZANGARO

Ter Nov 15, 2011 18:46
Álgebra Elementar
-
- Os valores de x são?
por Killder » Ter Nov 27, 2012 08:11
- 1 Respostas
- 2804 Exibições
- Última mensagem por Neperiano

Ter Nov 27, 2012 15:09
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
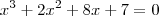 ,sabendo que o polinomio
,sabendo que o polinomio  é divisivel por x+1.
é divisivel por x+1.





![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.