 por fernandocez » Qui Mar 24, 2011 11:54
por fernandocez » Qui Mar 24, 2011 11:54
Pessoal mais uma. Essa eu fiz crente que tava indo bem, me deparei com um zero que acabou com a graça.
49) Um engenheiro vai projetar uma piscina em forma de paralelepípedo reto retângulo, cujas medidas internas são, em metros, expressas por x, x - 20 e 2. O maior volume que essa piscina poderá ter, em metros cúbicos, é:
resp: 200
Eu fiz assim:
V = 2x(x - 20)
2x² - 40x = 0
x = 0 ou
2x - 40 = 0
x = 20
Mas se x = 20 um dos lados é x - 20 que vai zerar.
Fiz pela opção (200) também deu raízes = 20 (delta = 0). Aonde errei?
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Qui Mar 24, 2011 12:31
por LuizAquino » Qui Mar 24, 2011 12:31
Analisando todos os seus tópicos, é fácil perceber que você tem a
mania de igualar tudo que vê pela frente a zero!

Se V(x) é o volume em função da medida x, então V(x)=0 seria a medida x que faz o volume ser zero, o que não é o desejado.
O que se quer é: qual é o valor máximo da função V(x)?
Aproveito para perguntar se as medidas no texto do exercício não seriam x,
20-x e 2 ? Se fossem essas medidas, você quer o máximo que a função
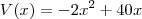
pode assumir.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fernandocez » Qui Mar 24, 2011 12:41
por fernandocez » Qui Mar 24, 2011 12:41
LuizAquino escreveu:Analisando todos os seus tópicos, é fácil perceber que você tem a
mania de igualar tudo que vê pela frente a zero!

Se V(x) é o volume em função da medida x, então V(x)=0 seria a medida x que faz o volume ser zero, o que não é o desejado.
O que se quer é: qual é o valor máximo da função V(x)?
Aproveito para perguntar se as medidas no texto do exercício não seriam x,
20-x e 2 ? Se fossem essas medidas, você quer o máximo que a função
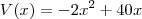
pode assumir.
O texto: "...expressas por x, x - 20 e 2. O maior volume que essa piscina poderá ter..." eu não sei se essa questão foi anulada.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Qui Mar 24, 2011 14:27
por LuizAquino » Qui Mar 24, 2011 14:27
Se as medidas forem realmente x, x-20 e 2, temos que o volume seria
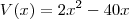
. Note que só faz sentido a medida x estar no intervalo aberto (0, 20). Para x nesse intervalo temos que V(x)<0, mas no contexto não faz sentido um volume negativo.
Desse modo, as medidas deveriam ser x, 20-x e 2. Para essas medidas, o volume seria
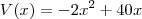
, que para x no intervalo (0, 20) é tal que V(x)>0. Além disso, o máximo dessa função seria V(10)=200.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fernandocez » Qui Mar 24, 2011 18:51
por fernandocez » Qui Mar 24, 2011 18:51
LuizAquino escreveu:Se as medidas forem realmente x, x-20 e 2, temos que o volume seria
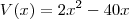
. Note que só faz sentido a medida x estar no intervalo aberto (0, 20). Para x nesse intervalo temos que V(x)<0, mas no contexto não faz sentido um volume negativo.
Desse modo, as medidas deveriam ser x, 20-x e 2. Para essas medidas, o volume seria
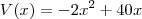
, que para x no intervalo (0, 20) é tal que V(x)>0. Além disso, o máximo dessa função seria V(10)=200.
Valeu Luiz, agora ficou claro prá mim. Obrigado.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 19:10
- 6 Respostas
- 3555 Exibições
- Última mensagem por fernandocez

Sáb Fev 26, 2011 22:29
Geometria Plana
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 23:27
- 3 Respostas
- 2497 Exibições
- Última mensagem por fernandocez

Dom Fev 27, 2011 10:33
Funções
-
- Questão prova concurso (sen e cos)
por fernandocez » Qua Mar 02, 2011 11:26
- 13 Respostas
- 9275 Exibições
- Última mensagem por fernandocez

Dom Mar 13, 2011 12:18
Trigonometria
-
- Questão prova concurso com Latitude
por fernandocez » Sáb Fev 26, 2011 23:38
- 2 Respostas
- 1823 Exibições
- Última mensagem por fernandocez

Qua Mar 02, 2011 11:27
Geometria Plana
-
- Questão prova concurso combinatória
por fernandocez » Ter Mar 01, 2011 12:35
- 2 Respostas
- 2671 Exibições
- Última mensagem por fernandocez

Qui Mar 03, 2011 22:47
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



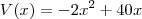 pode assumir.
pode assumir.
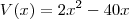 . Note que só faz sentido a medida x estar no intervalo aberto (0, 20). Para x nesse intervalo temos que V(x)<0, mas no contexto não faz sentido um volume negativo.
. Note que só faz sentido a medida x estar no intervalo aberto (0, 20). Para x nesse intervalo temos que V(x)<0, mas no contexto não faz sentido um volume negativo.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.