Pessoal mais uma. Essa eu fiz crente que tava indo bem, me deparei com um zero que acabou com a graça.
49) Um engenheiro vai projetar uma piscina em forma de paralelepípedo reto retângulo, cujas medidas internas são, em metros, expressas por x, x - 20 e 2. O maior volume que essa piscina poderá ter, em metros cúbicos, é:
resp: 200
Eu fiz assim:
V = 2x(x - 20)
2x² - 40x = 0
x = 0 ou
2x - 40 = 0
x = 20
Mas se x = 20 um dos lados é x - 20 que vai zerar.
Fiz pela opção (200) também deu raízes = 20 (delta = 0). Aonde errei?



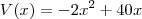 pode assumir.
pode assumir.
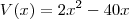 . Note que só faz sentido a medida x estar no intervalo aberto (0, 20). Para x nesse intervalo temos que V(x)<0, mas no contexto não faz sentido um volume negativo.
. Note que só faz sentido a medida x estar no intervalo aberto (0, 20). Para x nesse intervalo temos que V(x)<0, mas no contexto não faz sentido um volume negativo.