Estou com uma ED simples mas estou com uma duvida.
 =
= 
no caso troco o dx de lugar com o y e temos:
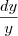 =
= 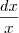
passo a integral dos dois lados
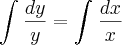
ai ficara
ln (y) = ln (x) + C
ai passo o e dos dois lados:
e elevado a ln y = e elevado a ln de x + o C
nesse caso ficaria
y = x + C
como C é constante posso substituir por A
y= x + A
só que ai que vem minha duvida, a reposta correta
é y= x.A
alguem pode me explicar o porque ??? obrigado


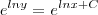
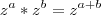


 concluimos que:
concluimos que:



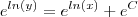
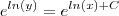


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)