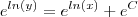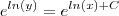por Higor » Seg Fev 21, 2011 13:12
por Higor » Seg Fev 21, 2011 13:12
Boa Tarde Galera.
Estou com uma ED simples mas estou com uma duvida.

=

no caso troco o dx de lugar com o y e temos:
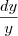
=
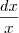
passo a integral dos dois lados
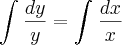
ai ficara
ln (y) = ln (x) + C
ai passo o e dos dois lados:
e elevado a ln y = e elevado a ln de x + o C
nesse caso ficaria
y = x + C
como C é constante posso substituir por A
y= x + A
só que ai que vem minha duvida, a reposta correta
é y= x.A
alguem pode me explicar o porque ??? obrigado
-
Higor
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Fev 20, 2011 17:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por Molina » Seg Fev 21, 2011 13:53
por Molina » Seg Fev 21, 2011 13:53
Boa tarde, Higor.
Você fez certo até aqui:
Higor escreveu:e elevado a ln y = e elevado a ln de x + o C
nesse caso ficaria
Veja a continuação:
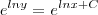
Pela propriedade de exponencial, temos que:
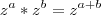
Foi isso que você se confundiu no lado direito. Com isso:


Tomando

concluimos que:


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Higor » Seg Fev 21, 2011 14:25
por Higor » Seg Fev 21, 2011 14:25
Molina muito obrigado pela ajuda.
Meu professor disse da seguinte maneira:
antes de fazer como voce fez :
e^ln y = e^ln(x+C)
ele sugeriu que
fosse feito assim:
e^ln y = e^ln x + ln e^C
ai como vc disse e ele tambem
multiplicação de base igual soma os expoentes e repete a base
e nesse caso
foi multiplicado os expoentes
ai chegou nessa resposta.
Essa passagem que ele faz antes chamando o C de ln e^C esta correto ???
-
Higor
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Fev 20, 2011 17:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por Molina » Seg Fev 21, 2011 14:39
por Molina » Seg Fev 21, 2011 14:39
Você está dizendo que daqui:

ele veio para cá:
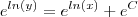
???
Se for isso, essa passagem está errada, pois para usar a propriedade exponencial, precisa haver uma multiplicação (e não uma soma, como há ali). Desta forma como está colocado aqui em cima, vamos chegar no resultado que você chegou primeiramente, onde o A está somando o x, e não multiplicando, como é a resposta correta.
Percebeu a diferença? O correto é elevar os dois lados da igualdade a base
e e desta forma, pela propriedade exponencial o lado direito fica com uma soma de expoentes que posteriormente abrimos na multiplicação das bases:

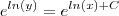


Caso não tenha ficado claro, avise.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Higor » Seg Fev 21, 2011 14:46
por Higor » Seg Fev 21, 2011 14:46
Molina mais uma vez obrigado.
Ficou muito claro, entendi certinho..

-
Higor
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Fev 20, 2011 17:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equaçao diferencial
por romulo39 » Dom Abr 03, 2011 20:58
- 1 Respostas
- 3933 Exibições
- Última mensagem por LuizAquino

Seg Abr 04, 2011 14:39
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial
por jacquelline » Qui Mai 17, 2012 11:04
- 2 Respostas
- 2067 Exibições
- Última mensagem por jacquelline

Sáb Mai 19, 2012 20:37
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial - 1
por Cleyson007 » Qua Nov 07, 2012 21:09
- 8 Respostas
- 3831 Exibições
- Última mensagem por MarceloFantini

Qui Nov 08, 2012 17:05
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial - 2
por Cleyson007 » Qua Nov 07, 2012 21:14
- 1 Respostas
- 1478 Exibições
- Última mensagem por e8group

Qua Nov 14, 2012 10:06
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial - 3
por Cleyson007 » Qua Nov 07, 2012 21:19
- 1 Respostas
- 1361 Exibições
- Última mensagem por young_jedi

Qui Nov 08, 2012 12:33
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 =
= 
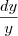 =
= 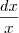
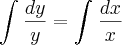


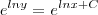
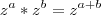


 concluimos que:
concluimos que: