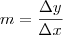
Você acha primeiro a equação da reta. Vou fazer aqui usando proporção:
Como julho/2000 passa a ser o ponto x=0 e julho/2001 é o ponto 12, nós temos dois pontos, (0; 35,6) e (12; 22), como está no gráfico, certo?
Como maio vem antes de julho, ele está nessa reta.
Então é só calcular, pegando um ponto genérico (x; y) na curva,

Então, a equação da reta fica:

Como julho/2001 é x=12; maio, que é dois meses antes, é x=10, então
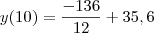

Espero que eu tenha ajudado,
Santa Lucci.







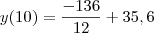




 que você viu (ou vai ver) em geometria analítica.
que você viu (ou vai ver) em geometria analítica.







![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)