Função Logarítmica

[OtavioBonassi]

O número de soluções da equação (todos os logs estão na mesma base, base 10) é :

a)0
b)1
c)2
d)3
e)4

Então, logo de cara o que eu fiz foi unir os dois logs antes do sinal de igual , então ficou assim :



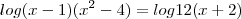
Ai então podemos "cancelar" os dois logs e igualar 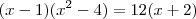, e multiplicando temos que , depois de um tempo ... , e aí que chega o caô , como resolver essa função do 3° grau ?! Estou sem idéias de como destrinchar isso ?! E avaliem se o que eu fiz até agora tá certo, posso ter viajado em alguma passagem.

Abraço,
Otávio.

[Pedro123]

Fala cara, blz??
entao, realmente, se vc tentar desenvolver essa equação, da um conta meio grande. O truque é o seguinte:
Lembrar do fato que x² - 4 = (x +2)(x-2) que ai sai suave a questao, abraços, qualquer duvida estamos ai

[OtavioBonassi]

Pô cara, valeu mesmo !! Não tinha nem passado perto da minha cabeça tentar simplificar desse jeito , obrigado mesmo !! E a solução é "apenas 1 resposta".


Acho que isso significa que aquela equação etc etc tem só 2 raízes reais ,mesmo sendo do 3° grau ? Ela só corta o eixo x em 2 pontos então ... tava fixado com a idéia de que "uma equação do 3o grau tem que ter 3 raízes".

[Pedro123]

Rapaz, na verdade não, realmente uma eq de 3 grau, possui 3 raizes, sendo que elas podem ser iguais (multiplicidade > 1 ou diferentes, tendo no caso três raizes diferentes,) na verdade, quando vc achou "apenas 1 solução" nao se refere à expressao do 3 grau, mas sim à solução da eq logaritmica, que é definida pelas soluçoes da equação do 3 grau, e pela condição de existencia dos logs. abraços, se não me engano é isso

[OtavioBonassi]

mas se por exemplo,se ao invés de ter simplificado e transformado a equação em uma do 2o grau eu tivesse deixado ela como sendo do 3o grau ,teoricamente daria certo também ,nao é ? E nesse caso eu teria 3 respostas ,ao invés de 2 ,mas mesmo assim a resposta teria que continuar sendo "apenas 1 resposta" ... voce sabe porque cara ? Será que se eu resolvesse essa eq. do 3o grau dariam 2 respostas iguais ou sei lá ,uma seria imcompatível ?

[Pedro123]

então cara, estava "brincando" aqui, e descobri que aquela equação possui 2 raizes iguais a -2. faça o seguinte, encontre as raizes da equação do 2º grau (a simplificada), essas serão 2 das raizes da eq do 3º grau. depois pegue a eq do terceiro grau e divida por x - (qualquer uma daz raizes, pela divisão de polinomios sabe?) vc vai chegar ou na mesma eq do segundo grau anterior, ou em uma diferente com 2 raizes iguais a -2, logo com delta = 0 , logo a eq possui sim 3 raizes, porem, 2 iguais.
abraços

[OtavioBonassi]

Maravilha cara !!! Mandou muito bem agora ... "luxou" mesmo ! Agora consegui ter segurança que os dois caminhos levam pro mesmo lugar haha ,valeu !

Abração ,
Otávio

[Pedro123]

kkk que isso, hsuahsu luxou foi massa kkkk qq coisa, tamos ai abras

[Renato_RJ]

Posso estar enganado, mas a sua equação no final não ficaria assim ?



Então, temos:




Estou certo ??

[OtavioBonassi]

então cara, na verdade voce teria isso aqui :



ai voce passaria o (x+2) pro outro lado dividindo, e sobraria :



o que vira uma eq. do segundo grau com 2 raízes !

O que eu tava discutindo com o Pedro123 é se tanto a equação do 3o grau quanto a do 2o levariam pro mesmo lugar ,e o Pedro123 comprovou que levam sim , só que é milhoes de vezes mais facil fazer uma do 2o grau

[Renato_RJ]

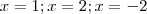
Boa sacada passar o para o outro lado da igualdade dividindo, facilita bastante o trabalho... Não tinha percebido isso, simplesmente analisei toda a equação...

Obrigado pela orientação.

[MarceloFantini]

Vocês estão lembrando as condições de existência? Satisfazer a equação logarítmica implica também que x satisfaça as condições de existência dos logaritmos.

[OtavioBonassi]

Exatamente por lembrar dessas condições que só tem 1 resposta possível hehe
Das duas raízes encotradas ,uma era +2 e a outra era um outro número ,portanto só temos 1 resposta .