 por gustavoluiss » Dom Nov 28, 2010 17:27
por gustavoluiss » Dom Nov 28, 2010 17:27
Um laço de 100 cm qual maior area de um retangulo que se pode formar?
é função do segundo grau.
-
gustavoluiss
- Colaborador Voluntário

-
- Mensagens: 118
- Registrado em: Ter Nov 23, 2010 15:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por alexandre32100 » Ter Nov 30, 2010 17:05
por alexandre32100 » Ter Nov 30, 2010 17:05
O que seria o "laço"? Seria o perímetro?
Se for, tem a fórmula de Herão:

, onde

é o semiperímetro, no caso

.

, mas ainda não achei nada que pudesse resolver.
-
alexandre32100
-
 por MarceloFantini » Ter Nov 30, 2010 19:05
por MarceloFantini » Ter Nov 30, 2010 19:05
A sua resolução não leva a muita coisa, pois carrega três incógnitas. Faça assim: monte um retângulo de dimensões x, x, 50-x e 50-x. A área é dada por

. Apenas encontre o vértice e pronto.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por alexandre32100 » Ter Nov 30, 2010 21:05
por alexandre32100 » Ter Nov 30, 2010 21:05
Por que seria este o triângulo de maior área?
-
alexandre32100
-
 por MarceloFantini » Qua Dez 01, 2010 00:05
por MarceloFantini » Qua Dez 01, 2010 00:05
Pois é o máximo da parábola. Quando ele disse laço eu entendi apenas um fio.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por alexandre32100 » Qua Dez 01, 2010 15:05
por alexandre32100 » Qua Dez 01, 2010 15:05
Hahaha. Nao acredito que li "triângulo" quando estava escrito retângulo. Desculpas aí, turma.
-
alexandre32100
-
 por MarceloFantini » Qua Dez 01, 2010 15:07
por MarceloFantini » Qua Dez 01, 2010 15:07
Acontece, não se preocupe!
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por alexandre32100 » Qua Dez 01, 2010 15:39
por alexandre32100 » Qua Dez 01, 2010 15:39
Mas, como é um retângulo, sejam x e y os lados destes, temos que
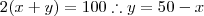
.
Daí
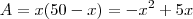
.
Agora sim entendi seu pensamento, Fantini.
-
alexandre32100
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função de segundo grau
por anfran1 » Qua Ago 15, 2012 16:23
- 6 Respostas
- 3560 Exibições
- Última mensagem por e8group

Qua Ago 15, 2012 20:39
Funções
-
- Função de segundo grau.
por Tatymtv » Ter Set 16, 2014 01:27
- 0 Respostas
- 1503 Exibições
- Última mensagem por Tatymtv

Ter Set 16, 2014 01:27
Funções
-
- Função de segundo grau simples
por Allanx » Sáb Mar 26, 2011 00:02
- 8 Respostas
- 4542 Exibições
- Última mensagem por Allanx

Dom Mar 27, 2011 00:10
Funções
-
- [DUVIDA]função de segundo grau
por julianafb » Ter Mar 05, 2013 01:33
- 1 Respostas
- 2600 Exibições
- Última mensagem por Russman

Ter Mar 05, 2013 02:04
Álgebra Linear
-
- Cálculo do lucro com função do segundo grau
por chenz » Qua Jun 02, 2010 10:07
- 2 Respostas
- 7359 Exibições
- Última mensagem por chenz

Qua Jun 09, 2010 11:00
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 , onde
, onde  é o semiperímetro, no caso
é o semiperímetro, no caso  .
. , mas ainda não achei nada que pudesse resolver.
, mas ainda não achei nada que pudesse resolver. . Apenas encontre o vértice e pronto.
. Apenas encontre o vértice e pronto.




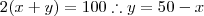 .
.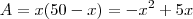 .
.

 , avisa que eu resolvo.
, avisa que eu resolvo.

