Dayse e
Cleyson,
boa noite!
Pensei da seguinte forma, mas, não garanto que seja a forma correta; afinal, esse assunto também não é o meu forte. [risos]
Fixemos um lugar para o professor (
x) ficar. Exemplo, na
primeira posição - que não existe, mas, vamos imaginar

: X,a,b,c,d,e,X,a,b,c,d,e,X
Com isso, vamos calcular apenas a permutação entre os alunos...
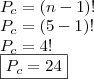
E, se o professor estivesse ocupando a
segunda posição: a,X,b,c,d,e,a,X,a,b,c,d,e,a,X
Calculemos as permutações...
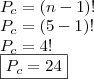
Se, fosse a
terceira posição: a,b,X,c,d,e,a,b,X,c,d,e,a,b,X
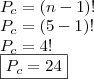
Se,
quarta posição: a,b,c,X,d,e,a,b,c,X,d,e,a,b,c,X
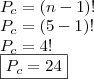
Enfim, a
quinta posição: a,b,c,d,X,e,a,b,c,d,X,e,a,b,c,d,X
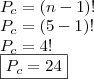
No enunciado, não foi dito qual o posicionamento do professor na mesa, então, temos aquelas possibilidades. Inclusive, vale ressaltar que quando

ocupa a
sexta posição ela coincide com a primeira, isto é, X,a,b,c,d,e,X,a,b,c,d,e,X = a,b,c,d,e,X,a,b,c,d,e,X,a,b,c,d,e,X.
Portanto,
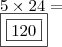





 : X,a,b,c,d,e,X,a,b,c,d,e,X
: X,a,b,c,d,e,X,a,b,c,d,e,X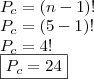
 ocupa a
ocupa a 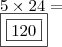


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.