 por Claudin » Qua Set 07, 2011 21:47
por Claudin » Qua Set 07, 2011 21:47
Gostaria de saber, sobre o simbolismo matemático na hora de representar soluções principalmente de inequações, quando utiliza-se parentese (), quando é colchete [], e também gostaria de saber sobre o "e" que simboliza o pertence, quando este "e" está invertido com um traço, ele significa o que?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qua Set 07, 2011 22:04
por MarceloFantini » Qua Set 07, 2011 22:04
Usamos parênteses quando o intervalo é aberto em algum extremo, ou seja, não contém o ponto. O colchete é quando o intervalo é fechado em algum extremo, logo contém o ponto. Sobre os símbolos: você fala deste
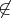
ou deste
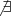
?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Qua Set 07, 2011 22:25
por Claudin » Qua Set 07, 2011 22:25
gostaria de saber o significado dos dois.

ps: o topico foi criado uas vezes, devido a falha na conexão, peço que apaguem um para melhor estética e organização do fórum!
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qua Set 07, 2011 22:28
por MarceloFantini » Qua Set 07, 2011 22:28
O primeiro significa não pertence. Em geral, um símbolo com um traço quer dizer sua negação, então = significa igual,

significa diferente. No caso do segundo,
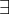
significa existe e portanto
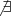
significa não existe.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Qua Set 07, 2011 22:38
por Claudin » Qua Set 07, 2011 22:38
Então como podeia me explicar sobre o sinal de nao pertence nesta solução sendo que foi encontrado resultado e na solução disse que nao pertence
- Anexos
-

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qua Set 07, 2011 22:57
por MarceloFantini » Qua Set 07, 2011 22:57
O conjunto
![[1,4] [1,4]](/latexrender/pictures/94fe668c80113341416b96929a8f1024.png)
é simplesmente o complementar de

. Se

, então
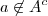
, que é seu complementar.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Qui Set 08, 2011 02:13
por Claudin » Qui Set 08, 2011 02:13
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Inequações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Linguagem matematica e algebra
por luiz syncode » Sex Jul 01, 2011 12:07
- 4 Respostas
- 2267 Exibições
- Última mensagem por LuizAquino

Ter Jul 05, 2011 23:04
Álgebra Elementar
-
- Linguagem algébrica
por Renatinha » Seg Nov 01, 2010 01:22
- 7 Respostas
- 5325 Exibições
- Última mensagem por girl

Ter Nov 02, 2010 14:06
Álgebra Elementar
-
- Linguagem algébrica
por Renatinha » Ter Nov 02, 2010 14:13
- 4 Respostas
- 4449 Exibições
- Última mensagem por Dinora

Dom Nov 07, 2010 23:24
Álgebra Elementar
-
- Matemática Financeira: matemática
por Victor Gabriel » Sex Mai 10, 2013 02:49
- 1 Respostas
- 3136 Exibições
- Última mensagem por killua05

Qua Mai 29, 2013 13:49
Matemática Financeira
-
- matemática
por sandi » Sáb Set 26, 2009 02:31
- 8 Respostas
- 5959 Exibições
- Última mensagem por sandi

Ter Set 29, 2009 20:41
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



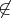 ou deste
ou deste 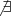 ?
?



 significa diferente. No caso do segundo,
significa diferente. No caso do segundo, 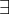 significa existe e portanto
significa existe e portanto 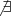 significa não existe.
significa não existe.


![[1,4] [1,4]](/latexrender/pictures/94fe668c80113341416b96929a8f1024.png) é simplesmente o complementar de
é simplesmente o complementar de  . Se
. Se  , então
, então 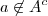 , que é seu complementar.
, que é seu complementar.


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.