Tetraedro - Motivo que os vértices formam base e coordenadas

[rochadapesada]

a letra "a", eu respondi que, como ele forma um tetraedro, eles (os vetores) tem que ser LI e portanto formam uma base (Não sei se estou certo)

a "b" não conseguir desenvolver

[Russman]

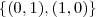Sim. Um conjunto de vetores é base de um espaço se, e somente se, este conjunto é LI e GERA o espaço. Isto é, os vetores desse espaço se escrevem de FORMA ÚNICA como combinação linear dos vetores da base.

Exemplo: Por que que gera o ?

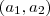Gera poque o conjunto é LI( a solução de 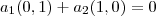é apenas 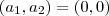) e existe apenas um par de números reais 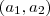tais que um vetor pertença a . É fácil de mostrar. Suponha que 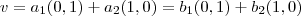. Assim,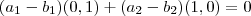



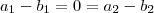Mas, como o conjunto é LI a única solução possível dessa equação é de modo qu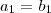e e 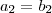. Portanto, o vetor se escreve de forma única.

[rochadapesada]

Estou dando geometria analítica, não cheguei em álgebra linear ainda :/ ... Ai essa questão é para responder com geometria analítica

[Russman]

Qual a definição de base que te apresentaram?

[rochadapesada]

O básico que 3 vetores tem que ser LI, que a norma de u é a raiz de a1^2+a2^2+a3^2 apenas isso... peguei do livro tratamento vetorial...

[Russman]

Isso não é suficiente e nem necessário pra definir base.

[e8group]

Define-se Base na álgebra linear( vide livro http://toandaihoc.files.wordpress.com/2 ... lgebra.pdf página 41 ) da seguinte forma :

" Definition. Let V be a vector space. A basis for V is a linearly inde­
pendent set of vectors in V which spans the space V. The space V is finite­
dimensional if it has a fim:te basis."

Entretanto há um resultado A.L. que diz se é um espaço vetorial de dimensão finita,digamos ,então qualquer subconjunto de linearmente independente cuja cardinalidade é constitui-se uma base para .

Como em G.A. em geral trabalhamos no ( máximo n = 3) , é um espaço vetorial de dimensão finita que és .Desta forma podemos definir base utilizando o resultado acima . De acordo com o livro de G.A . o qual já mencionei , lá defini-se base p/ V^3 como tripla ordenada .

[Russman]

" Definition. Let V be a vector space. A basis for V is a linearly inde­
pendent set of vectors in V which spans the space V. The space V is finite­
dimensional if it has a fim:te basis."

Entretanto há um resultado A.L. que diz se é um espaço vetorial de dimensão finita,digamos ,então qualquer subconjunto de linearmente independente cuja cardinalidade é constitui-se uma base para .

espaço

Perfeito. A base é um conjunto LI que gera o espaço. Veja que se o conjunto é LI e subconjunto do espaço então este pode ser uma base.