 por Abner » Qua Mai 11, 2011 17:32
por Abner » Qua Mai 11, 2011 17:32
Prove que: Se P(A) = 0 , então
P(AU B) = P(B)
.
-
Abner
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Qua Jan 26, 2011 18:48
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Qua Mai 11, 2011 23:28
por MarceloFantini » Qua Mai 11, 2011 23:28
Se
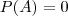
, então

. O que é

? Se souber isso, responderá a questão.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por lanca » Dom Mai 15, 2011 00:46
por lanca » Dom Mai 15, 2011 00:46
Oi Abner estou com a mesma duvida na mesma questão..se encontrar um caminho posta aqui por favor...
Estou tentando a da Tomografia..
obrigada
-
lanca
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Mai 15, 2011 00:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
 por MarceloFantini » Dom Mai 15, 2011 00:54
por MarceloFantini » Dom Mai 15, 2011 00:54
Vocês não podem ter medo de demonstrações, essa é trivial: sabemos que

. Se
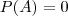
, então

e portanto
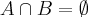
, e leva a relação inicial a
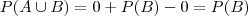
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por lanca » Dom Mai 15, 2011 01:26
por lanca » Dom Mai 15, 2011 01:26
Oi Marcelo..
Posso colocara assim
P(A)= 0 Logo A é um conjunto vazio, portanto AUB=B, então P(AUB) = P(B)
-
lanca
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Mai 15, 2011 00:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
 por MarceloFantini » Dom Mai 15, 2011 01:28
por MarceloFantini » Dom Mai 15, 2011 01:28
Pode, é outra forma.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por lanca » Dom Mai 15, 2011 01:36
por lanca » Dom Mai 15, 2011 01:36
Obrigada Marcelo...
Foi de grande valia sua ajuda!!!
-
lanca
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Mai 15, 2011 00:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
 por lanca » Dom Mai 15, 2011 01:41
por lanca » Dom Mai 15, 2011 01:41
Por favor me orienta nessa questão:
Prove a seguinte afirmação, assumindo que A
e B são eventos com P(A)>0 e P(B)>0:
P(A|B)>P(A) se e só se P(B|A)>P(B) se e só se P(A?B)>P(A)P(B).
Neste caso, dizemos que A e B são eventos positivamente correlacionada
-
lanca
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Mai 15, 2011 00:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
 por MarceloFantini » Dom Mai 15, 2011 01:43
por MarceloFantini » Dom Mai 15, 2011 01:43
Essa questão já foi posta em outro tópico, procure entre os do Abner.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por lanca » Dom Mai 15, 2011 01:45
por lanca » Dom Mai 15, 2011 01:45
Eu estou terminando..vou postar aqui vc da uma olhada?
-
lanca
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Mai 15, 2011 00:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
 por MarceloFantini » Dom Mai 15, 2011 01:50
por MarceloFantini » Dom Mai 15, 2011 01:50
Não, poste no outro tópico. Evite colocar duas questões no mesmo tópico, isso diminui clareza e evita a vantagem de facilitar a busca depois.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Abner » Dom Mai 15, 2011 13:10
por Abner » Dom Mai 15, 2011 13:10
Marcelo fiz da maneira como vc postou...obrigado pela ajuda....
-
Abner
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Qua Jan 26, 2011 18:48
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Abner » Dom Mai 15, 2011 13:12
por Abner » Dom Mai 15, 2011 13:12
Ianca tb estou quebrando a cabeça na questão das matrizes....
-
Abner
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Qua Jan 26, 2011 18:48
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Abner » Dom Mai 15, 2011 13:13
por Abner » Dom Mai 15, 2011 13:13
Ianca tb estou quebrando a cabeça na questão das matrizes....
-
Abner
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Qua Jan 26, 2011 18:48
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Abner » Dom Mai 15, 2011 22:58
por Abner » Dom Mai 15, 2011 22:58
Tendo uma matriz de ordem 3x3 e outra 3x4 como obter a matriz aumentada?
-
Abner
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Qua Jan 26, 2011 18:48
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por lanca » Dom Mai 15, 2011 23:47
por lanca » Dom Mai 15, 2011 23:47
Oi Abner...
E ai conseguiu alguma coisa da matriz...
Vc viu eu postei a resposta do ex 3 no outro forum...
a resposta do 1...eu acho que não é P(AUBB)= P(A) +P(B) [b]- P( A inter B) acho que é + p( A inter B)
-
lanca
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Mai 15, 2011 00:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
 por MarceloFantini » Dom Mai 15, 2011 23:53
por MarceloFantini » Dom Mai 15, 2011 23:53
Pessoal, evitem discutir múltiplas dúvidas num mesmo tópico, crie outro para isso. Ajuda a organização do fórum!
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Abner » Dom Mai 15, 2011 23:59
por Abner » Dom Mai 15, 2011 23:59
Eu vi e tb fiz da mesma forma...quanto ao exer 1 a formula é -(AinterB)
Só não estou conseguindo desenvolver o exer de matriz aumentada...tem alguma ideia...
-
Abner
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Qua Jan 26, 2011 18:48
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por lanca » Seg Mai 16, 2011 00:06
por lanca » Seg Mai 16, 2011 00:06
Abner..não consegui nenhum item dessa atividade...
Já li tdo material de apoio e nada...
voltando ao ex. anterior eu acho que é +P( A inter B)..PQ se tirarmos o n. da intersecção..ele tbem não fara parte da união..ai como justificar a união se vc exclui um termo do conjunto.
-
lanca
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Mai 15, 2011 00:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
 por lanca » Seg Mai 16, 2011 00:25
por lanca » Seg Mai 16, 2011 00:25
Abner é menos mesmo...refiz com números...
-
lanca
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Mai 15, 2011 00:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
 por lanca » Seg Mai 16, 2011 00:39
por lanca » Seg Mai 16, 2011 00:39
Marcelo, desculpa...
-
lanca
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Mai 15, 2011 00:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Probabilidade] Exercício Desafio de Probabilidade
por werwer » Qua Mar 21, 2012 18:57
- 0 Respostas
- 10348 Exibições
- Última mensagem por werwer

Qua Mar 21, 2012 18:57
Estatística
-
- Probabilidade - Função Densidade de Probabilidade
por pimgui » Qua Dez 16, 2020 10:53
- 0 Respostas
- 21652 Exibições
- Última mensagem por pimgui

Qua Dez 16, 2020 10:53
Probabilidade
-
- Probabilidade - função probabilidade
por tarlix » Ter Mai 24, 2011 12:41
- 1 Respostas
- 5345 Exibições
- Última mensagem por Neperiano

Dom Out 16, 2011 17:00
Estatística
-
- [Probabilidade] probabilidade de obj com estudantes
por fenixxx » Seg Ago 13, 2012 14:06
- 1 Respostas
- 4521 Exibições
- Última mensagem por Neperiano

Ter Out 09, 2012 10:10
Probabilidade
-
- [probabilidade condicional] probabilidade de gol.
 por Mr_ MasterMind » Sáb Set 19, 2015 17:35
por Mr_ MasterMind » Sáb Set 19, 2015 17:35
- 0 Respostas
- 4534 Exibições
- Última mensagem por Mr_ MasterMind

Sáb Set 19, 2015 17:35
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 . Se
. Se 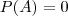 , então
, então  e portanto
e portanto 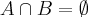 , e leva a relação inicial a
, e leva a relação inicial a 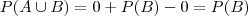 .
.




















![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.