A questão:
Sejam a e b números reais tais que
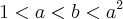 . Se
. Se  ,
, 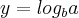 ,
, 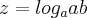 e
e  então:
então:a)
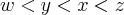
b)

c)

d)

e)
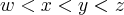
Gabarito: A
Minha resolução:

 (1)
(1)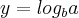
 (2)
(2)Substituindo (1) em (2):


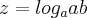



Assim, se x = 3, teríamos y = 1/3; z = 4; w = 2/3 ou ainda,
se x = 4; y = 1/4; z = 5; w = 3/4
Ou seja, y < w < x < z (alternativa d)
Fiz uma planilha no Excel que confirma o gabarito (alternativa A). Queria entender onde errei.
Grato.


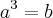 , o que, pela condição citada acima, está errado. Assim, testando vários valores, temos que um x que satisfaz aquela desigualdade é, por exemplo, x = 3/2. Assim, temos:
, o que, pela condição citada acima, está errado. Assim, testando vários valores, temos que um x que satisfaz aquela desigualdade é, por exemplo, x = 3/2. Assim, temos:  , fato que respeita a condição e nos leva a alternativa A. Confira!
, fato que respeita a condição e nos leva a alternativa A. Confira!

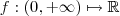 definida por
definida por  para algum
para algum  fixado (que cumpre com a desigualdade dada) .Como esta função admite inversa à esquerda ela é injetora (pois , se
fixado (que cumpre com a desigualdade dada) .Como esta função admite inversa à esquerda ela é injetora (pois , se  , tem-se
, tem-se  ) e assim ela é estritamente monótona (estritamente crescente ou estritamente decrescente ) .Como
) e assim ela é estritamente monótona (estritamente crescente ou estritamente decrescente ) .Como 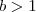 ,segue que
,segue que  é estritamente crescente ,ou seja , se
é estritamente crescente ,ou seja , se  e
e 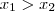 então
então  (*) .
(*) .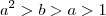 então
então 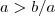 então
então 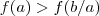 (**) .
(**) . 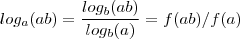 (***) e
(***) e 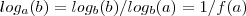 . (****)
. (****) em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.