 por maria cleide » Seg Ago 29, 2011 22:39
por maria cleide » Seg Ago 29, 2011 22:39
O gráfico da função quadrática
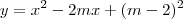
, sendo m um número inteiro não negativo, não intersepta o eixo x em nenhum ponto. Então o valor mínimo que essa função assume é:
A-( ) 1
B-( )4
C-( )0
D-( )1/2
Eu sei que
delta é maior ou igual a zero. Mas não sei resolver
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por MarceloFantini » Ter Ago 30, 2011 09:05
por MarceloFantini » Ter Ago 30, 2011 09:05
Você está errada. Se a função
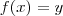
não intercepta o eixo x em nenhum ponto, não há raízes, e portanto o discriminante é menor que zero. O seu valor mínimo será atingido no vértice da parábola, visto que ela tem "boca para cima". Para encontrar, use que a abscissa do vértice é dada por
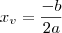
, e coloque isso na função para encontrar seu valor.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por maria cleide » Ter Ago 30, 2011 11:30
por maria cleide » Ter Ago 30, 2011 11:30
Apliquei
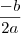
achei

e não consegui prosseguir, por favor me explique como continuo.
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por MarceloFantini » Ter Ago 30, 2011 11:45
por MarceloFantini » Ter Ago 30, 2011 11:45
Substituindo, temos
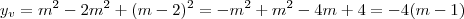
. Agora, note que como delta é negativo, temos

e por m ser inteiro não-negativo,

. O único valor que satisfaz é
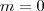
, e logo
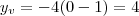
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por maria cleide » Ter Ago 30, 2011 22:34
por maria cleide » Ter Ago 30, 2011 22:34
Você encontrou
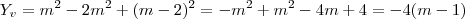
, mas de onde tirou esses valores sendo que
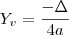
que dá
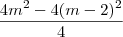
?
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por MarceloFantini » Qua Ago 31, 2011 08:51
por MarceloFantini » Qua Ago 31, 2011 08:51
Verifique que
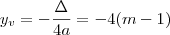
. Faça as contas e verá que é a mesma coisa. Tome cuidado pois
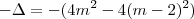
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função quadrática
por Ananda » Sex Mar 28, 2008 16:00
- 6 Respostas
- 9224 Exibições
- Última mensagem por admin

Sex Mar 28, 2008 21:25
Funções
-
- Função quadratica
por Aline » Qui Jun 18, 2009 14:22
- 2 Respostas
- 2628 Exibições
- Última mensagem por Cleyson007

Sex Jun 19, 2009 10:00
Funções
-
- Função Quadratica
por Aline » Qui Jun 18, 2009 14:37
- 1 Respostas
- 2010 Exibições
- Última mensagem por Marcampucio

Qui Jun 18, 2009 16:45
Funções
-
- Função Quadratica
por Aline » Sáb Jun 20, 2009 18:23
- 1 Respostas
- 2089 Exibições
- Última mensagem por Molina

Dom Jun 21, 2009 20:28
Funções
-
- Função Quadratica
 por guijermous » Sáb Abr 10, 2010 10:02
por guijermous » Sáb Abr 10, 2010 10:02
- 4 Respostas
- 8033 Exibições
- Última mensagem por Molina

Sáb Abr 10, 2010 16:27
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
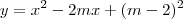 , sendo m um número inteiro não negativo, não intersepta o eixo x em nenhum ponto. Então o valor mínimo que essa função assume é:
, sendo m um número inteiro não negativo, não intersepta o eixo x em nenhum ponto. Então o valor mínimo que essa função assume é: 
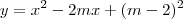 , sendo m um número inteiro não negativo, não intersepta o eixo x em nenhum ponto. Então o valor mínimo que essa função assume é:
, sendo m um número inteiro não negativo, não intersepta o eixo x em nenhum ponto. Então o valor mínimo que essa função assume é: 
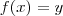 não intercepta o eixo x em nenhum ponto, não há raízes, e portanto o discriminante é menor que zero. O seu valor mínimo será atingido no vértice da parábola, visto que ela tem "boca para cima". Para encontrar, use que a abscissa do vértice é dada por
não intercepta o eixo x em nenhum ponto, não há raízes, e portanto o discriminante é menor que zero. O seu valor mínimo será atingido no vértice da parábola, visto que ela tem "boca para cima". Para encontrar, use que a abscissa do vértice é dada por 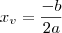 , e coloque isso na função para encontrar seu valor.
, e coloque isso na função para encontrar seu valor.

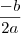 achei
achei  e não consegui prosseguir, por favor me explique como continuo.
e não consegui prosseguir, por favor me explique como continuo.
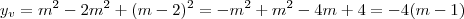 . Agora, note que como delta é negativo, temos
. Agora, note que como delta é negativo, temos  e por m ser inteiro não-negativo,
e por m ser inteiro não-negativo,  . O único valor que satisfaz é
. O único valor que satisfaz é 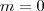 , e logo
, e logo 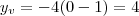 .
.

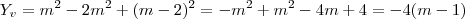 , mas de onde tirou esses valores sendo que
, mas de onde tirou esses valores sendo que 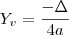 que dá
que dá 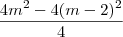 ?
?
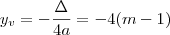 . Faça as contas e verá que é a mesma coisa. Tome cuidado pois
. Faça as contas e verá que é a mesma coisa. Tome cuidado pois 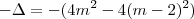 .
.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.